Intro
안녕하세요, 오늘은 지난 글에서 소개한 HNE(Heterogeneous Network Embedding) 에 중에서 Proximity-Preserving methods에 대해서 정리해보겠습니다.
proximity는 무엇일까요? 사전 상의 의미는 _가까움_입니다. 그래프 임베딩은 그래프의 목적은 topological information (위치, 연결 정보)을 보존하는 것이라고 말씀드렸죠? 그런 의미에서 Proximity-Preserving methods를 해석하면 실제 그래프 상에서 node들이 가까운 정도를 보존하면서 임베딩을 수행하는 방법들이라고 할 수 있고, 이는 topological information을 보존하는 하나의 방법으로 볼 수 있습니다. 그 외에 방법들에 대해서는 다음 글에서 정리하도록 하겠습니다.
이번 글 역시 heterogeneous network representation learning a unified framework with survey and benchmark 논문의 내용을 정리합니다.
논문에서 설명하는 Proximity-Perseving methods는 크게 random walk based approaches와 first/second order proximity based approaches가 있습니다. 오늘은 이 두 접근법들 중 random walk baed approaches에 대해서 정리해보겠습니다.
한글표현과 영어표현이 아래와 같이 섞여서 사용될 수 있습니다
그래프, 네트워크: graph, network (두 단어는 interchangeable)
객체: node
연결: edge
Random walk based approaches
Metapath
Random walk based approaches를 이해하기 위해서는 meta path라는 것에 대해서 알 필요가 있습니다. HN (Heterogeneous Network)는 여러 type의 node와 edge로 구성된 복잡한 그래프 입니다. 이 그래프 상의 임의의 node $n_0$ 에서 연결된 edge를 따라 $m-1$번 이동해서 다른 node $n_m$에 도착했다고 가정해보죠. 그러면 아래와 같은 path가 생성될 겁니다.
$$n_0 \xrightarrow{e_1} n_1 \xrightarrow{e_2} \dots \xrightarrow{e_{m-1}} n_{m-1} \xrightarrow{e_m} n_m$$
여기서, $k$번째 node의 type을 $o_k$, edge의 type을 $l_k$로 하겠습니다. 그러면 위의 path는 다시 아래와 같이 표현이 가능해지죠
$$o_0 \xrightarrow{l_1} o_1 \xrightarrow{l_2} \dots \xrightarrow{l_{m-1}} o_{m-1} \xrightarrow{l_m} o_m$$
바로 위와 같이 표현된 node와 edge의 type을 만족하는 path들을 meta path라고 합니다. 각각의 $o_k, l_k$에는 같은 type의 node, edge라면 무엇이든 올 수 있습니다. (물론 실제로 edge로 이어진 것들만 가능합니다.)
metapath2vec
이제 Random walk based approach중 하나인 metapath2vec에 대해서 이해할 준비가 되었습니다.
사전에 정의된
metapath $$M=o_0 \xrightarrow{l_1} o_1 \xrightarrow{l_2} \dots \xrightarrow{l_{m-1}} o_{m-1} \xrightarrow{l_m} o_m$$이 있습니다.
이제 HN상의 모든 node $v\in V$에 대해서, 위 $M$의 형태를 갖는 metapath를 생성해내는 겁니다. node당 몇 개의 metapath를 만들지는 hyperparameter로 설정할 수 있습니다. 이러한 방법의 조상 격 방법인 DeepWalk의 경우 node당 10개의 metapath를 생성했습니다.
경우에 따라서 한 node로 부터 만들 수 있는 ($M$의 형태를 만족하는) path는 매우 많아질 수 있기 때문에, 우리는 random walk를 통해서 수많은 가능한 path 중 10개 정도를 뽑습니다.
만약 type이 $o_{i-1}$인 $i-1$번째 node $n_{i-1}$에서 type이 $o_i$인 $i$번째 node $n_i$를 결정할 때, $n_{i-1}$과 edge type이 $l_i$인 edge로 연결된 여러 node들 $N_{n_{i-1}}^{l_{i}}$이 있으면, $\frac{1}{|N_{n_{i-1}}^{l_{i}}|}$의 확률로 하나를 선택하게 됩니다.
자 그럼 이제 이렇게 해서 각 node $v\in V$별로 $M$의 형태를 갖는 여러 path들인 $P={P_1, P_2, \dots, P_{K}}, (K=|V| \times 10)$를 얻었습니다. 그럼 우리는 이제 얻은 path에 있는 node들의 embedding을 아래 objective function을 따라서 최적화하게 됩니다.
$$\mathcal{J}=\sum_{v\in V}\sum_{u\in \mathcal{C(v)}}\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})}$$
$C(v)$는 node $v$의 context입니다. context는 random walk로 생성한 path $P_k \in P$에서, 대상 node의 앞, 뒤에 존재하는 node들을 의미합니다. 이 또한 앞, 뒤로 몇 개씩의 node를 context로 볼 지는 hyperparameter로 설정할 수 있으며, 그 크기를 _window size_라고합니다. window size가 2라면, 생성한 path에서 대상 node의 앞, 뒤로 2개씩 총 4개의 node를 context로 보겠다는 뜻입니다.
위 objective상에서는 각 node별로 context에 대해서 최적화한다고 표현이 되어있지만, 실제 구현할 때는 만들어진 path를 stride하면서 기준 node와 그 앞 뒤 node들을 context로 보고 최적화하지 않을까 예상됩니다.
위의 objective는 최대화해야하는 대상으로, 생성한 path상에 존재하는 각 node에 대해서 그 node와 그 node의 context node들의 embedding dot product가 모든 non-context node들에 대한 dot product의 합에 대해서 높은 비율을 갖도록하는 것이 목표입니다.
metapath2vec은 여기서 한 가지 variant를 더 만드는 데요, 바로 대상 node $v$의 context $C(v)$에서 여러 번 발견되는 context node $u$에는 더 큰 weight $W_{vu}$를 부여하는 것 입니다.
$$\mathcal{J}=\sum_{v\in V}\sum_{u\in \mathcal{C(v)}}w_{vu}\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})}$$
마지막으로, 위 objective를 더 빠르게 최적화 할 수 있는 방법도 있습니다. negative sampling이라는 방법인데요, 비단 metapath2vec 뿐만 아니라 위 objective처럼 softmax형태를 띄는 objective를 최적화 할 때 많이 대체되는 방법입니다. 위 objective에서, 분모부분인 $\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})$의 계산은 expensive하기 때문에, 모든 node를 고려하지 않고 이를 approximate할 수 있는 방법인 negative sampling을 사용합니다.
HIN2Vec
이 논문에서는 HN을 HIN(Heterogeneous Information Network)라고 표현했습니다.
HIN2Vec이 최적화 하려고 하는 parameters는 3개의 embedding matrix $W_X, W_Y, W_R$입니다. $W_X, W_Y \in R^{|V| \times d}$는 source node embedding과 target node embedding이고, $W_R \in R^{|L| \times d}$는 고려하고자 하는 모든 $M$의 각 embedding입니다. ($|L|$은 고려하고자 하는 모든 $M$의 종류 수)
node $u, v$의 embedding은 각각 $e_u = W_X^u, e_v = W_Y^v$, 그리고 $M$의 embedding은 $e_r = f_{01}(W_R^M), f_{01}(.) = normalize func.$가 됩니다.
HIN2Vec은 학습을 위해서 random walk를 통해 positive tuple인 $(u, v, M)$을 찾습니다. node $u$와 $v$가 meta-path $M$을 통해 연결되어있다는 걸 뜻합니다. 그리고 여러 개의 random node $u^{'}$와 함께 아래의 objective를 최적화합니다.
$$\mathcal{J}=\sum_{(u, v, M)}\log{p(M|u, v)} + \sum_{(u^{'}, v, M)}\log{(1 - p(M|u^{'}, v))}$$
$$=\sum_{(u, v, M)}\left(\log{\sigma(e_u^T A_M e_v)} + \sum_{u^{'}}\log{\sigma(-e_{u^{'}}^T A_M e_v)}\right)$$
$A_M$은 $e_r$의 값으로 만든 diagonal matrix입니다. 위의 object 또한 negative sampling 형식이며 아래의 softmax값을 approximate합니다.
$$\mathcal{J}=\sum_{M}\sum_{(u, v)\in V}w_{uv}^M\log\frac{exp(e_{u}^{T} A_M e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}A_M e_{v})}$$
마무리
오늘 정리한 metapath2vec, HIN2Vec말고도 여러 random walk 기반의 proximity-preserving methods가 있습니다. 논문에 첨부된 표를 인용하면서 이번 글 마치겠습니다!
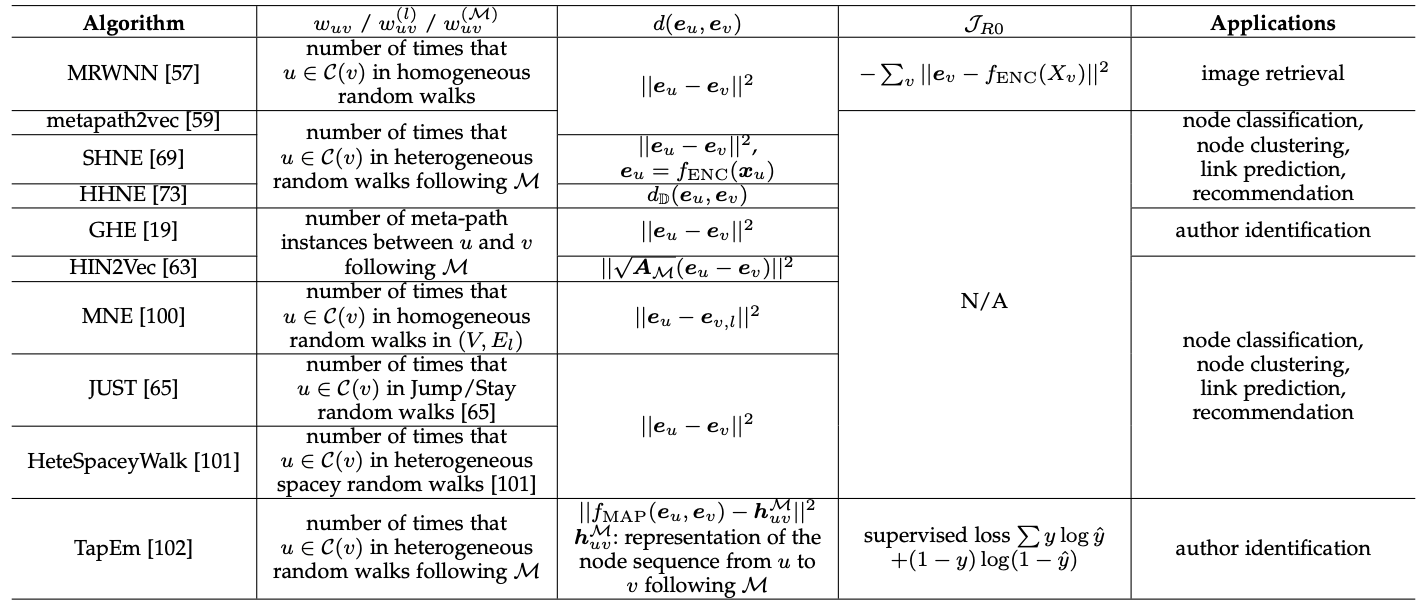
감사합니다.
References
Heterogeneous Network Representation Learning: A Unified Framework with Survey and Benchmark
metapath2vec: Scalable Representation Learning for Heterogeneous Networks
HIN2Vec: Explore Meta-paths in Heterogeneous Information Networks for Representation Learning
'[Machine Learning]' 카테고리의 다른 글
| HNE - proximity preserving methods(2) (0) | 2021.09.27 |
|---|---|
| HNE (Heterogeneous Network Embedding) - 소개 (0) | 2021.08.31 |
| AWS (2) Services (0) | 2021.05.12 |
| AWS (1) 시작하기 (0) | 2021.04.27 |