TwoPark

Intro

안녕하세요, 지난 글에서는 소개한 HNE(Heterogeneous Network Embedding) Proximity-Preserving methods 중 random walk based approaches에 대해서 정리했는데요, 오늘은 이어서 First/Second-Order Proximity Based Approaches에 대해서 정리하겠습니다.

이번 글 역시 heterogeneous network representation learning a unified framework with survey and benchmark 논문의 내용을 정리합니다.

First/Second-Order Proximity based approaches는 비교적 간단해서, First/Second-Order Proximity based approaches에 대해서 정리한 뒤 Proximity-Preserving methods에 대한 부가적인 내용을 추가해서 정리하겠습니다.

한글표현과 영어표현이 아래와 같이 섞여서 사용될 수 있습니다

그래프, 네트워크: graph, network (두 단어는 interchangeable)
객체: node
연결: edge

Random walk based approaches vs. First/Second-Order Proximity based approaches

Random walk based approaches와 First/Second-Order Proximity Based Approaches의 차이는 무엇일까요? 제 주관적인 의견을 적어보겠습니다.

Random walk based approaches는 주로 source node로 부터 random walk를 수행해서 주어진 meta path의 모양을 갖는 path들을 찾았는데요, 이를 이용하면 여러 hop 떨어진 node사이의 관계도 고려할 수 있게 됩니다. 하지만 random walk를 수행하는 임의성이 있기 때문에, source node와 1 hop관계를 갖는 node라 할 지 라도 선택받지 못할 수 있습니다.

반면에 First/Second-Order Proximity Based Approaches의 경우에는 이름에도 적혀있듯이, 각 source node의 1 or 2 hop 관계의 모든 node를 고려합니다. 대신 이 경우 Random walk based approaches와 달리 여러 hop (>2) 관계에 있는 node들의 관계는 학습에 사용되지 않습니다.

그래서 저는 데이터만 충분하다면 여러 hop을 고려할 수 있는 random walk based 기반 방법이 더 좋지 않을까? 생각합니다.

HNE는 아니지만 개인적인 프로젝트에서 random walk based approach인 Deepwalk와 first/second-order proximity based approach인 LINE을 사용했을 때, Deepwalk이 더 좋은 성능을 보였던 경험이 있기도 합니다.

First/Second-Order Proximity based approaches

PTE

PTE는 Predictive Text Embedding의 약자로, NLP분야에서 사용되는 HNE기법입니다. PTE는 여러 개의 edge type $l \in L$이 있을 때, 각 edge type만으로 이루어진 sub graph (bipartite graph)를 만든 뒤에 각 graph별로 node embedding을 최적화합니다. objective는 아래와 같습니다.

$$\mathcal{J}=\sum_{l \in L}\sum_{u, v\in V}w_{uv}^l\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V_{\phi(u)}}exp(e_{u^{'}}^{T}e_{v})}$$

$w_{uv}^l$은 type이 $l$인 edge로 연결된 node $u, v$사이의 weight입니다. 연결이 있으면 0이상의 값이, 없으면 0을 갖습니다. $V_{\phi(u)}$는 $u$와 같은 type인 node의 집합입니다. 그리고 위 objective는 결국 edge type에 대해서 aggregation이 가능해서, 아래와 같이 변형가능합니다.

$$\mathcal{J}=\sum_{u, v\in V}w_{uv}\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V_{\phi(u)}}exp(e_{u^{'}}^{T}e_{v})}, w_{uv}=\sum_{l}w_{uv}^l$$

이처럼 PTE는 다소 간단한 방법이라고 볼 수 있습니다.

AspEm

AspEm는 PTE에서 한단계 발전한 모델입니다. 각 edge type별로 sub graph를 만들었던 PTE와 달리, 사전에 정의된 Aspect에 해당하는 edge type들로 이루어진 sub graph를 만들고, 이들을 각각 최적화합니다.

여기서 aspect는 사용자가 정의하기 나름인데요, 예를들어 영화 dataset인 IMDB dataset으로 만든 HN이 user, movie, actor, director, genre 5가지 edge type으로 이루어져 있다고 하겠습니다. 그러면 여기서 user가 좋아하는 actor를 위주로 embedding을 수행하고 싶다면, 우리는 node로는 user, movie, actor node type인 node를 갖고, edge는 user-movie, movie-actor를 잇는 edge type만으로 이루어진 sub graph를 추출해서 이를 최적화하면 됩니다.

edge type의 집합 $L$이 있을 때, 이것의 부분 집합으로 한 aspect $a$에 대한 edge type의 집합은 $L^a \subseteq L$입니다.

따라서 각 aspect $a$에 대한 sub graph의 embedding 최적화는 아래 objective에 따라 이루어 집니다.

$$\mathcal{J}=\sum_{l \in L^a}\frac{1}{Z_l}\sum_{u, v\in V}w_{uv}^l\log\frac{exp(e_{u, a}^{T}e_{v, a})}{\sum_{u^{'}\in V_{\phi(u)}}exp(e_{u^{'},a}^{T}e_{v,a})}$$

HEER

Heterogeneous information network Embedding via Edge Representations의 약자입니다 ㅋㅋ 되게 기네요.

HEER 역시 PTE의 변형으로, edge type별 embedding도 함께 학습하는 특징이 있습니다. objective는 아래와 같습니다.

$$\mathcal{J}=\sum_{l \in L}\sum_{u, v\in V}w_{uv}^l\log\frac{exp(\mu_l^Tg_{uv})}{\sum_{u^{'}, v^{'}\in P_l(u, v)} exp(\mu_l^Tg_{u^{'}v^{'}})}$$

$\mu_l$은 edge type $l$의 embedding이고, $g_{uv}$는 node $u, v$의 edge embedding으로 $g_{uv}=e_u \odot e_v$ 입니다. ($\odot$: element wise product)

이때, $\mu_l$의 원소를 대각성분으로 갖는 diagonal matrix $A_l$을 사용해서 아래와 같은 bilinear form으로 변형할 수 있게 됩니다.

$$\mathcal{J}=\sum_{l \in L}\sum_{u, v\in V}w_{uv}^l\log\frac{exp(e_u^T A_l e_v)}{\sum_{u^{'}, v^{'}\in P_l(u, v)} exp(e_{u^{'}}^T A_l e_{v^{'}})}$$

그 외

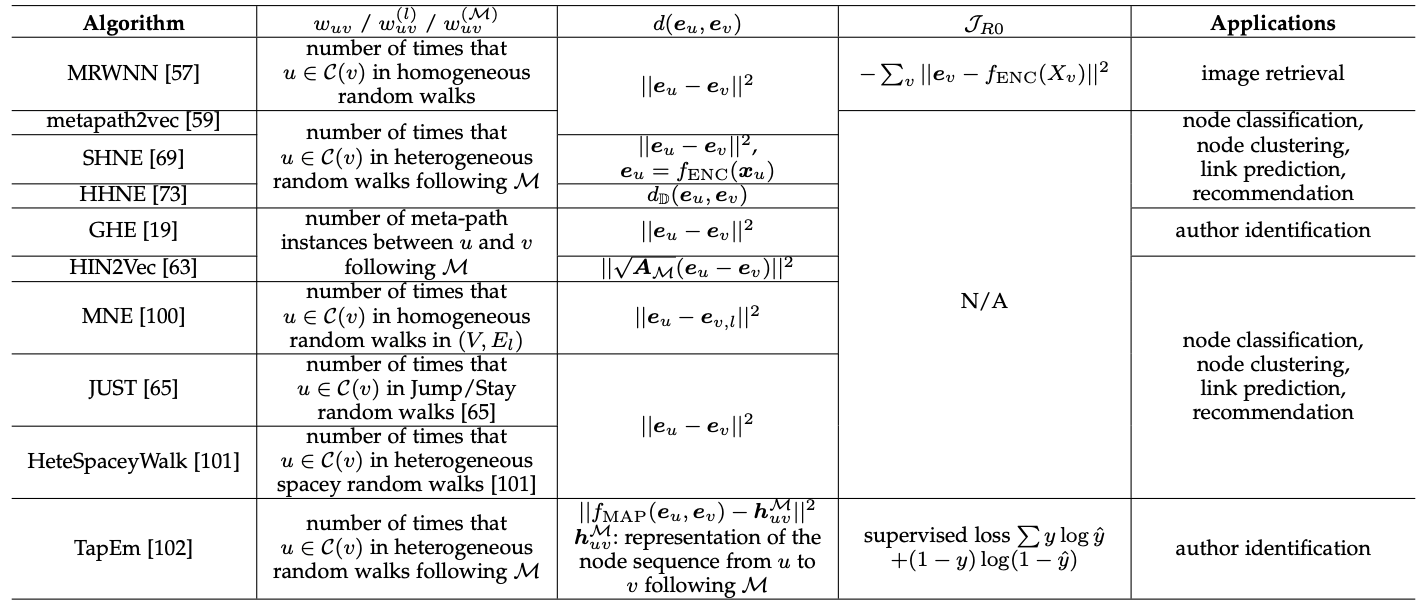
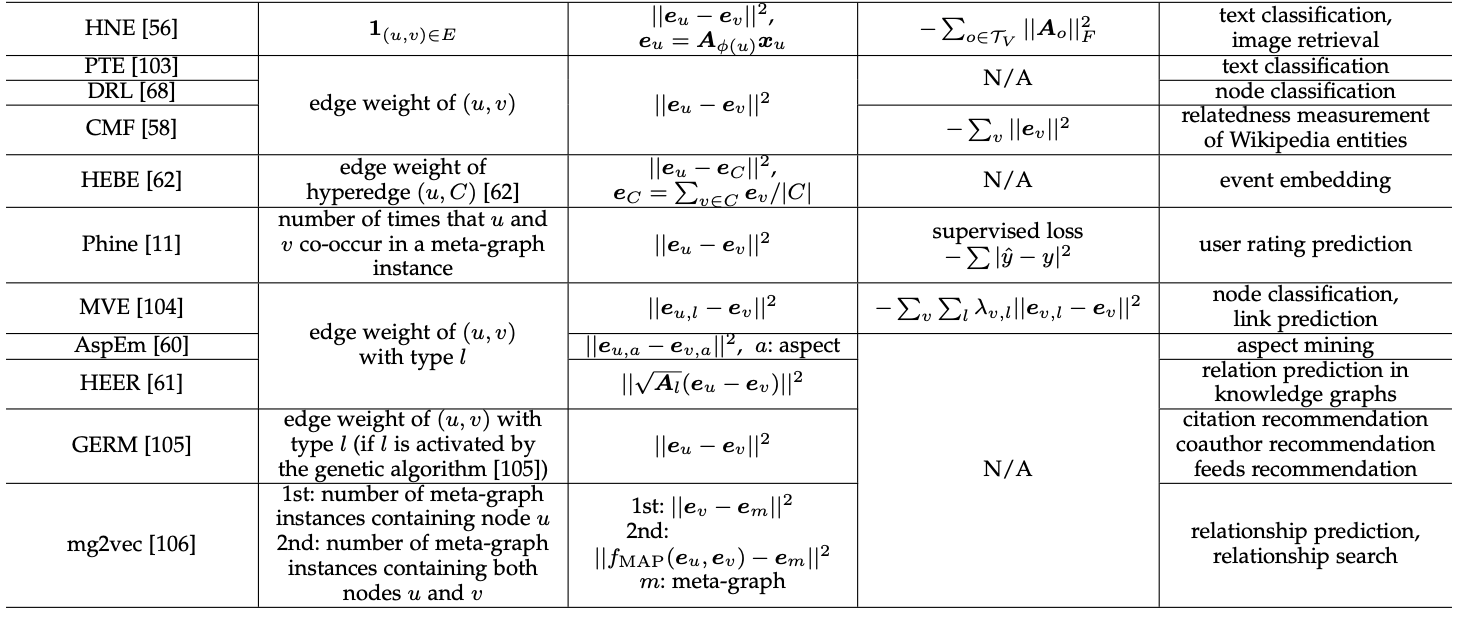
위에서 설명한 3가지 모델을 포함해서 나머지 First/Second-Order Proximity based approaches를 정리한 표를 논문에서 인용해서 첨부하겠습니다.

Network Smoothness Enforcement

여기까지 Proximity-Preserving methods에 대해서 대략적인 정리를 해봤습니다. 논문의 저자들은 흥미로운 insight를 제시했는데요, 우선 여러 모델의 objective는 아래와 같이 일반화 할 수 있습니다.

$$max \mathcal{J}=\sum_{u, v\in V}w_{uv}\log\frac{s(u, v)}{\sum_{u^{'}}s(u', v)} + \mathcal{J}_{R_0}$$

$s(u, v)$는 node $u, v$의 유사도를 나타내는 함수로, $f(e_u)^Tf(e_v)$로 나타낼 수 있습니다. 대부분의 method는 $f$를 항등 함수로 사용하겠지만, HIN2Vec는 $f(e_u)=\sqrt{M}e_u$, HEER은 $f(e_u)=\sqrt{A_l}e_u$이 될 수 있습니다. (왜 bilinear form으로 변형했는지 알 수 있는 대목입니다!)

위 식을 negative sampling 형태로 변환 한뒤, 정리를 하면, $\mathcal{J}_{R_0}$외에 2가지 regulization term을 발견할 수 있습니다.

마지막 수식을 보면, 결국 대부분의 HNE 모델의 objective는 1) 두 node $u, v$의 embedding이 유사해지고 (빨간 박스 첫번째 줄), 2) $u, v$의 embedding의 크기가 0보다 커지게 하고, (빨간 박스 두번째 줄) 3) $u$가 아닌 나머지 $u^{'}$에 대해서는 v와 유사해지지 않도록 (빨간 박스 세번째 줄) 최적화가 됩니다.

1)은 objective의 주 목적이고, 2)는 $u, v$의 embedding이 모두 zero vector 되지 않도록 하고, 3)은 모든 node의 embedding이 동일해지지 않도록 하는 역할을 하게 됩니다.

단순히 수식만 재배열 했을 뿐인데 이런 insight을 얻을 수 있네요.

마무리

오늘은 여러 First/Second-Order Proximity based approaches를 정리하고, 대부분의 HNE 모델들이 갖는 objective에 대한 insight을 정리해봤습니다.

사실 proximity-preserving 모델들은 shallow하다고 볼 수 있습니다. 최적화학 모델의 layer가 1개만 있는 거죠. 그러다 보니 non-linearity가 부족한 특징이 있습니다.

다음에는 조금 더 deep한 모델들을 사용하는, Message-passing methods에 대해서 정리하겠습니다.

감사합니다!

References

Heterogeneous Network Representation Learning: A Unified Framework with Survey and Benchmark
PTE: Predictive Text Embedding through Large-scale Heterogeneous Text Networks
ASPEM: Embedding Learning by Aspects in Heterogeneous Information Networks
Easing Embedding Learning by Comprehensive Transcription of Heterogeneous Information Networks

Intro

안녕하세요, 오늘은 지난 글에서 소개한 HNE(Heterogeneous Network Embedding) 에 중에서 Proximity-Preserving methods에 대해서 정리해보겠습니다.

proximity는 무엇일까요? 사전 상의 의미는 _가까움_입니다. 그래프 임베딩은 그래프의 목적은 topological information (위치, 연결 정보)을 보존하는 것이라고 말씀드렸죠? 그런 의미에서 Proximity-Preserving methods를 해석하면 실제 그래프 상에서 node들이 가까운 정도를 보존하면서 임베딩을 수행하는 방법들이라고 할 수 있고, 이는 topological information을 보존하는 하나의 방법으로 볼 수 있습니다. 그 외에 방법들에 대해서는 다음 글에서 정리하도록 하겠습니다.

이번 글 역시 heterogeneous network representation learning a unified framework with survey and benchmark 논문의 내용을 정리합니다.

논문에서 설명하는 Proximity-Perseving methods는 크게 random walk based approaches와 first/second order proximity based approaches가 있습니다. 오늘은 이 두 접근법들 중 random walk baed approaches에 대해서 정리해보겠습니다.

한글표현과 영어표현이 아래와 같이 섞여서 사용될 수 있습니다

그래프, 네트워크: graph, network (두 단어는 interchangeable)
객체: node
연결: edge

Random walk based approaches

Metapath

Random walk based approaches를 이해하기 위해서는 meta path라는 것에 대해서 알 필요가 있습니다. HN (Heterogeneous Network)는 여러 type의 node와 edge로 구성된 복잡한 그래프 입니다. 이 그래프 상의 임의의 node $n_0$ 에서 연결된 edge를 따라 $m-1$번 이동해서 다른 node $n_m$에 도착했다고 가정해보죠. 그러면 아래와 같은 path가 생성될 겁니다.

$$n_0 \xrightarrow{e_1} n_1 \xrightarrow{e_2} \dots \xrightarrow{e_{m-1}} n_{m-1} \xrightarrow{e_m} n_m$$

여기서, $k$번째 node의 type을 $o_k$, edge의 type을 $l_k$로 하겠습니다. 그러면 위의 path는 다시 아래와 같이 표현이 가능해지죠

$$o_0 \xrightarrow{l_1} o_1 \xrightarrow{l_2} \dots \xrightarrow{l_{m-1}} o_{m-1} \xrightarrow{l_m} o_m$$

바로 위와 같이 표현된 node와 edge의 type을 만족하는 path들을 meta path라고 합니다. 각각의 $o_k, l_k$에는 같은 type의 node, edge라면 무엇이든 올 수 있습니다. (물론 실제로 edge로 이어진 것들만 가능합니다.)

metapath2vec

이제 Random walk based approach중 하나인 metapath2vec에 대해서 이해할 준비가 되었습니다.

사전에 정의된

metapath $$M=o_0 \xrightarrow{l_1} o_1 \xrightarrow{l_2} \dots \xrightarrow{l_{m-1}} o_{m-1} \xrightarrow{l_m} o_m$$이 있습니다.

이제 HN상의 모든 node $v\in V$에 대해서, 위 $M$의 형태를 갖는 metapath를 생성해내는 겁니다. node당 몇 개의 metapath를 만들지는 hyperparameter로 설정할 수 있습니다. 이러한 방법의 조상 격 방법인 DeepWalk의 경우 node당 10개의 metapath를 생성했습니다.

경우에 따라서 한 node로 부터 만들 수 있는 ($M$의 형태를 만족하는) path는 매우 많아질 수 있기 때문에, 우리는 random walk를 통해서 수많은 가능한 path 중 10개 정도를 뽑습니다.
만약 type이 $o_{i-1}$인 $i-1$번째 node $n_{i-1}$에서 type이 $o_i$인 $i$번째 node $n_i$를 결정할 때, $n_{i-1}$과 edge type이 $l_i$인 edge로 연결된 여러 node들 $N_{n_{i-1}}^{l_{i}}$이 있으면, $\frac{1}{|N_{n_{i-1}}^{l_{i}}|}$의 확률로 하나를 선택하게 됩니다.

자 그럼 이제 이렇게 해서 각 node $v\in V$별로 $M$의 형태를 갖는 여러 path들인 $P={P_1, P_2, \dots, P_{K}}, (K=|V| \times 10)$를 얻었습니다. 그럼 우리는 이제 얻은 path에 있는 node들의 embedding을 아래 objective function을 따라서 최적화하게 됩니다.

$$\mathcal{J}=\sum_{v\in V}\sum_{u\in \mathcal{C(v)}}\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})}$$

$C(v)$는 node $v$의 context입니다. context는 random walk로 생성한 path $P_k \in P$에서, 대상 node의 앞, 뒤에 존재하는 node들을 의미합니다. 이 또한 앞, 뒤로 몇 개씩의 node를 context로 볼 지는 hyperparameter로 설정할 수 있으며, 그 크기를 _window size_라고합니다. window size가 2라면, 생성한 path에서 대상 node의 앞, 뒤로 2개씩 총 4개의 node를 context로 보겠다는 뜻입니다.

위 objective상에서는 각 node별로 context에 대해서 최적화한다고 표현이 되어있지만, 실제 구현할 때는 만들어진 path를 stride하면서 기준 node와 그 앞 뒤 node들을 context로 보고 최적화하지 않을까 예상됩니다.

위의 objective는 최대화해야하는 대상으로, 생성한 path상에 존재하는 각 node에 대해서 그 node와 그 node의 context node들의 embedding dot product가 모든 non-context node들에 대한 dot product의 합에 대해서 높은 비율을 갖도록하는 것이 목표입니다.

metapath2vec은 여기서 한 가지 variant를 더 만드는 데요, 바로 대상 node $v$의 context $C(v)$에서 여러 번 발견되는 context node $u$에는 더 큰 weight $W_{vu}$를 부여하는 것 입니다.

$$\mathcal{J}=\sum_{v\in V}\sum_{u\in \mathcal{C(v)}}w_{vu}\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})}$$

마지막으로, 위 objective를 더 빠르게 최적화 할 수 있는 방법도 있습니다. negative sampling이라는 방법인데요, 비단 metapath2vec 뿐만 아니라 위 objective처럼 softmax형태를 띄는 objective를 최적화 할 때 많이 대체되는 방법입니다. 위 objective에서, 분모부분인 $\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})$의 계산은 expensive하기 때문에, 모든 node를 고려하지 않고 이를 approximate할 수 있는 방법인 negative sampling을 사용합니다.

HIN2Vec

이 논문에서는 HN을 HIN(Heterogeneous Information Network)라고 표현했습니다.

HIN2Vec이 최적화 하려고 하는 parameters는 3개의 embedding matrix $W_X, W_Y, W_R$입니다. $W_X, W_Y \in R^{|V| \times d}$는 source node embedding과 target node embedding이고, $W_R \in R^{|L| \times d}$는 고려하고자 하는 모든 $M$의 각 embedding입니다. ($|L|$은 고려하고자 하는 모든 $M$의 종류 수)

node $u, v$의 embedding은 각각 $e_u = W_X^u, e_v = W_Y^v$, 그리고 $M$의 embedding은 $e_r = f_{01}(W_R^M), f_{01}(.) = normalize func.$가 됩니다.

HIN2Vec은 학습을 위해서 random walk를 통해 positive tuple인 $(u, v, M)$을 찾습니다. node $u$와 $v$가 meta-path $M$을 통해 연결되어있다는 걸 뜻합니다. 그리고 여러 개의 random node $u^{'}$와 함께 아래의 objective를 최적화합니다.

$$\mathcal{J}=\sum_{(u, v, M)}\log{p(M|u, v)} + \sum_{(u^{'}, v, M)}\log{(1 - p(M|u^{'}, v))}$$
$$=\sum_{(u, v, M)}\left(\log{\sigma(e_u^T A_M e_v)} + \sum_{u^{'}}\log{\sigma(-e_{u^{'}}^T A_M e_v)}\right)$$

$A_M$은 $e_r$의 값으로 만든 diagonal matrix입니다. 위의 object 또한 negative sampling 형식이며 아래의 softmax값을 approximate합니다.

$$\mathcal{J}=\sum_{M}\sum_{(u, v)\in V}w_{uv}^M\log\frac{exp(e_{u}^{T} A_M e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}A_M e_{v})}$$

마무리

오늘 정리한 metapath2vec, HIN2Vec말고도 여러 random walk 기반의 proximity-preserving methods가 있습니다. 논문에 첨부된 표를 인용하면서 이번 글 마치겠습니다!

감사합니다.

References

Heterogeneous Network Representation Learning: A Unified Framework with Survey and Benchmark
metapath2vec: Scalable Representation Learning for Heterogeneous Networks
HIN2Vec: Explore Meta-paths in Heterogeneous Information Networks for Representation Learning

Intro

안녕하세요, 오늘은 머신 러닝 알고리즘의 한 종류인 HNE(Heterogeneous Network Embedding) 에 대해서 정리해보겠습니다.

네트워크, 그래프라고 알려져 있는 자료구조는 여러 객체 사이의 관계를 표현하는데 매우 효과적입니다.

어떤 객체와 직접/ 간접적으로 연결되어있는 객체들을 분석하면 우리는 이 객체와 유사한 객체들을 찾을 수 있습니다.

하지만 문제가 있습니다. 직접/ 간접적인 연결이 너무 많다는 겁니다. 이는 우리가 일일이 다 고려할 수 없는 수준이죠.

어떤 객체는 10개의 다른 객체와 연결되어 있는 반면, 어떤 객체는 10,000개의 다른 객체와 연결되어있기도 합니다. 간접적인 연결까지 다 고려하면 이루 말할 수 없는 다양한 연결 관계가 존재합니다.

따라서 그래프 (또는 네트워크)는 그동안 다루기 어려운 자료구조로 여겨져 왔습니다. 이 복잡한 관계를 분석하려면 많은 연산이 필요하니까요!

하지만 머신 러닝 기술이 발전하고 하드웨어 스펙이 좋아지면서, 이 까다로운 자료구조를 다룰 수 있는 기술이 등장합니다.

바로 그래프 임베딩 (Graph Embedding) 입니다.

저는 그래프 임베딩 중에서도, 그래프를 구성하는 node와 edge의 종류가 여러 개인 Heterogeneous network (graph) embedding 에 대해서 공부해서 정리하려고 합니다.

heterogeneous network representation learning a unified framework with survey and benchmark 라는 논문의 내용을 정리할 거고, 내용이 많아서 여러 개에 나눠서 하려고 합니다.

한글표현과 영어표현이 섞여서 사용될 수 있습니다. 아래 단어 사전을 참고하세요.

• 그래프, 네트워크: graph, network (두 단어는 구분없이 사용됩니다.)
• 객체: node
• 연결: edge

Graph Embedding

그래프 임베딩은 그래프를 구성하는 객체들을 낮은 차원의 벡터로 표현하는 기술입니다.

$N$개의 객체 (node)로 이루어진 그래프를 있는 그대로 표현하려면, 적어도 $N \times N$크기의 인접 매트릭스가 필요합니다. 그래서 어느 두 객체가 연결되어 있으면 (edge가 존재하면) 해당 부분은 1, 아니면 0으로 채워지게 되는 것이죠. 물론 edge에 가중치 (weight)가 있거나, edge에 방향이 있는지 (directed), 없는지 (undirected)에 따라서 달라집니다.

그리고 이 인접 매트릭스는 매우 sparse하기 때문에 (대부분이 0이기 때문에), 낭비되는 메모리도 크고, 많은 연산량을 필요로 합니다. 그리고 직접적인 연결 정보만을 알 수 있죠. 이 인접 매트릭스만으로는 그래프의 직접/ 간접적인 풍부한 연결정보를 모두 파악하기 어렵습니다.

하지만 그래프 임베딩 기술을 적용한다면, $N \times d,, (d << N)$인 매트릭스의 각 값에, 다른 객체들 사이의 직접/ 간접적인 연결 정보를 고려한 값을 채울 수 있습니다. 각 객체는 $d$차원의 벡터로 표현이 되는데, 이때 그래프 상에서의 구조적 정보 (topological information)을 보존하는 형태로 표현이 됩니다. 그래프 상에서 가까우면, 비슷한 벡터로 표현이 된다는 뜻 입니다.

이렇게 그래프를 구성하는 각 node가 표현된 $d$차원 벡터를 latent vector, 또는 node의 representation이라고 합니다. 그래프 임베딩은 이 latent vector를 어떻게 구하느냐에 따라 여러 방법이 존재합니다.

수식으로 표현하면 $${\Phi}: V \rightarrow \mathcal{R}^{|V|\times d}$$

그래프 임베딩의 가장 시초격인 방법은 DeepWalk입니다. 그래프 임베딩에 관심이 있으신 분이라면 꼭 논문을 읽어보시길 추천드립니다.

HNE (Heterogeneous Network Embedding)

Intro에서 잠깐 말씀드렸듯이, heterogeneous network는 그래프를 구성하는 node와 edge의 종류가 여러개인 그래프입니다. 조금 더 복잡하지만, 더 풍부한 표현이 가능합니다. 구글에서 사용한다고 알려진 지식 그래프 (knowledge graph) 도 heterogeneous graph의 한 종류 입니다.

HNE를 위해서는 node의 type을 고려해야 합니다. 따라서 수식이 아래와 같이 달라집니다.

$${\Phi}_k: V_k \rightarrow \mathcal{R}^{|V_k|\times d}$$

여기서 $k$는 여러 개의 node type 중 $k$번째 type을 의미합니다. 이런식으로 HNE는 각 type의 node들의 latent vector를 학습하는 방법입니다.

마무리

오늘은 그래프 임베딩은 무엇인지, 그리고 HNE는 또 무엇인지 정리해봤습니다.

사실 그래프 임베딩은 node 뿐만 아니라 edge를 임베딩할 수도 있고, 그래프 전체를 embedding할 수 있습니다. 하지만 대부분의 경우 node embedding을 목표로 합니다.

다음 글에서는 조금 더 자세히, HNE는 어떤 방법들이 있는지 정리하겠습니다.

감사합니다!

• [지난 글] AWS ①  AWS 시작하기
• AWS ②  Services - SageMaker를 중심으로
• AWS ③  영화 추천 어플리케이션 제작 및 실습

 안녕하세요, 이번 시간에는 AWS에서 Machine Learning 기반 어플리케이션을 제작하고, 배포하기 위해서 사용되는 주요 서비스들을 정리하려고 합니다.

 아래 사진은 AWS에서 제공하는 서비스들을 일부 캡처한 것입니다. 보시는 바와 같이, 다양한 목적에 따라 세분화된 걸 볼 수 있습니다. 따라서 Machine Learning 기반 어플리케이션을 제작, 배포하기 위해서는 여러 서비스를 함께 사용해야 합니다.

 이번 글에서는 제가 실습에 사용했던 서비스들만 정리하도록 하겠습니다. 이것들만 있어도 Machine Learning 기반 어플리케이션을 제작, 배포할 수 있습니다. 위 사진에서 이미 즐겨찾기 되어있네요 ㅎㅎ.

• EC2 (Elastic Compute Cloud)
  • 한 줄 요약 - 클라우드의 가상 서버
  • GPU가 없는 나만의 컴퓨터라고 생각할 수 있습니다. (GPU는 특수한 업무를 수행할 때만 필요하므로, 따로 그 업무를 실행할 때 설정해서 사용할 수 있습니다.)
  • 필요에 따른 CPU, RAM, 네트워크 사양에 따라 적절한 EC2 intance를 생성하면, 사용가능합니다.  
• IAM (Identity and Acess Management)
  • 한 줄 요약 - 사용자 엑세스 및 암호화 키 관리
  • 우리처럼 튜토리얼 수준이 아닌, 여러 명이 AWS를 활용해서 대규모 프로젝트를  수행할 수 있죠, 이때 명시적인 역할 분담을 돕는 서비스가 IAM이라고 할 수 있습니다. (1명인 경우에도 IAM은 필요합니다! root 처럼요.)
  • IAM을 사용해서 협업하는 사람들의 역할을 정하고, 각각 사용할 수 있는 서비스, 자원 등의 접근 권한을 부여합니다. 그래야 혹시 모를 자원의 낭비나, 실수로 인한 피해를 방지할 수 있죠!
  • policy (정책), user (사용자), role (역할)을 설정해서 사용할 수 있습니다.
• Cloud9
  • 한 줄 요약 - 클라우드 기반 IDE (통합 개발 환경)
  • 코드의 작성, 실행 및 디버깅을 위한 IDE를 클라우드 (web) 상에서 다룰 수 있게 해주는 서비스입니다.
  • Cloud9 instance를 생성할 때, IDE를 실행할 EC2 instance도 함께 만들어집니다.
  • 터미널을 통한 data 다운로드 및 코드 실행 (application 배포까지)도 가능합니다.
• S3 (Simple Storage Service)
  • 한 줄 요약 - 클라우드 기반 데이터 저장소
  • 우리가 프로젝트를 진행할 때, 필요한 데이터를 저장하고 검색할 수 있는 기능을 지원하는 서비스입니다.
  • 예를 들어, 아래에 있는 SageMaker의 jupyter notebook instance를 통해서 training dataset을 다운로드 할 때, 다운로드 받을 파일이 저장된 위치나, 다운로드한 파일을 저장할 S3 instance (bucket이라고도 합니다.) 의 주소?를 통해 접근할 수 있습니다.   
• SageMaker (Sage: 현자)
  • 한 줄 요약 - Machine Learning 모델의 구축, 학습, 및 배포
  • Cloud9에서, Machine Learning과 관련된 기능을 따로 때왔다고 볼 수 있습니다.
  • 크게 jupyter notebook, inference (endpoint)로 구성되어있습니다.
  • 다양한 기능을 수행할 수 있는 GUI를 제공하지만, jupyter notebook instance에서 EDA, 모델 훈련, 모델 배포 등 거의 대부분의 기능을 수행할 수 있습니다.
    • EDA를 위한 기본적인 library가 설치되어있고, 터미널도 지원합니다.
  • 모델을 배포해서 새로운 data에 대해서 inference를 수행하기 위해서는 endpoint가 필요합니다.
    • 새로운 data를 학습된 모델에게 전달하고, 그 output을 다시 돌려주는 역할을 합니다.  
• Lambda
  • 한 줄 요약 - 배포된 어플리케이션의 트래픽 자동 관리
  • 어플리케이션을 배포하는 걸로 끝이 아닙니다. Cloud9 instance를 통해 어플리케이션을 성공적으로 배포했다고 해도, Cloud9이 구동되는 EC2 instance의 사양은 동적으로 변하지 않고 그대로 입니다.
  • 하지만 우리가 배포한 어플리케이션을 사용하고자 하는 사용자들은 몰릴 때도 있고, 그렇지 않을 때도 있죠.
  • 따라서 트래픽이 변해도 안정적으로 어플리케이션을 서비스할 수 있도록, 부하를 관리해주는 load balancer 역할을 해주는 서비스가 Lambda 입니다.

이렇게 실습을 위해 필요한 AWS 서비스들에 대한 정리가 끝났습니다!

다음 글부터는 본격적인 실습에 들어가면서, 이 글에서 소개해드린 서비스들이 어떻게 서로 연결되어서, 하나의 어플리케이션을 배포할 수 있게 되는지 정리해보겠습니다.

글 읽어주셔서 감사합니다!

처음 시작한 블로그의 첫 글을 무엇으로 할지 고민하다가, 요즘 공부를 시작한 AWS (Amazon Web Service)에 대해서 정리를 하기로 했습니다.

 AWS는 웹 서비스를 쉽게 제작, 배포할 수 있도록 다양한 클라우드 기반 서비스를 제공해주고 있는데요, 요즘 많은 기업에서 AWS를 사용해서 서비스를 제공하고 있고, AWS를 다뤄본 경험이 있는 사람을 우대하는 공고가 많이 있더라고요. 

 물론 해당 직무 역량이 더 중요하겠지만, AWS가 얼마나 좋길래 많은 기업들에서 우대하는지 궁금하고, 알아두면 좋을 거 같아서 공부를 결심했습니다.

 저는 대학원에서 추천 시스템을 연구하기도 해서 AWS로 머신 러닝을 활용한 서비스를 어떻게 제작, 배포할 수 있을지 알아봤어요. 다행스럽게도 아마존에서 이를 위한 학습 커리큘럼을 제공해서, 이를 참고해서 공부를 시작했습니다.

 저 커리큘럼을 따라가면 단순히 AWS 사용법 뿐만 아니라 머신 러닝에 대한 지식도 쌓을 수 있습니다. 머신 러닝에 대한 배경 지식이 부족하다고 생각하시는 분들은 커리큘럼을 따라가면 되고, 머신 러닝에 대한 어느 정도 배경이 있으신 분들은 관심 있는 주제만 골라서 들으면 될 거 같아요.

 저는 모든 강의를 듣지 않고 띄엄띄엄 들었지만, 이 강의에서 많은 걸 배울 수 있었어요. 이 강의부터 본격적으로 AWS를 사용해서 머신 러닝 서비스를 제작, 배포해보는 실습을 할 수 있거든요.

 실습이 포함되어 있기 때문에, AWS를 사용하기 위한 비용이 지출될 수 있어요. 저는 AWS 프리티어를 통해서 비용 지출 없이 실습을 완료했습니다.

주의! 프리티어를 사용한다고 모든 서비스가 무료가 아니니, 홈페이지를 참고해서 사용하려는 서비스의 무료 사용 기준을 확인하세요.

 위 강의의 마지막 실습에 중요한 것들이 다 모여있기 때문에, 마지막 실습 위주로, 부족한 설명은 이전의 강의를 참고해서 내용을 정리하려고 합니다.

 AWS를 다룰 예정인 분들은 저 강의를 직접 듣는 걸 추천드리고요, 단지 저처럼 AWS에 대한 호기심을 가진 정보의 분이라면 제가 쓴 글을 먼저 보는 것도 도움이 될 거라고 생각합니다. (도움이 되도록 노력할게요...!)

 우선 계획한 글의 순서는 아래와 같습니다. 

• AWS ①  AWS 시작하기
• AWS ②  Services - SageMaker를 중심으로
• AWS ③  영화 추천 서비스 제작 및 실습

 다음 글에서는, 실습에 앞서서 알아야할 AWS의 서비스들에 대해서 정리한 뒤, 3번째 글부터 본격적인 실습을 정리해 보겠습니다.

읽어주셔서 감사합니다.