Intro
오늘은 두 변수 사이의 상관관계에 대해서 정리하겠습니다. 상관관계는 한 변수가 분할에 따른 다른 변수의 변화를 관찰해서, 두 변수가 함께 움직이면 양의 상관관계, 두 변수가 반대로 움직이면 음의 상관관계를 갖는다고 말합니다.

주의: 양/음의 상관관계는 두 변수의 "인과관계"를 의미하지 않습니다.
이전 글에서 아이스크림 가게의 매출을 예시로 변수의 평균과 분산, 표준편차에 대해서 알아봤는데요, 만약 아이스크림 가게 A의 다음날 매출을 예측하고 싶을 때, 아이스크림 가게의 매출에 영향을 주는 요소는 어떤게 있을까요?
날씨
계절
코로나 거리두기 단계
...
우리는 이런 다양한 요소들을 고려해서 매출을 예측할 수 있습니다.
이때 우리가 예측하고자 하는 아이스크림 가게 매출을 target(또는 목푯값), 이를 예측하기 위해 사용하는 요소를 feature(또는 예측값)이라고 합니다.
변수 사이의 상관관계는 한 변수의 값의 변화에 따른 다른 변수의 변화를 관찰할 수 있습니다. 이는 _(1) target과 feature_에 대해서 수행할 수도 있고, _(2) feature와 다른 feature_에 대해서 수행할 수 있습니다.
(1) target과 feature의 상관관계: 어떤 feature가 변하면 target은 어떻게 변하는지 알 수 있기 때문에, target을 예측하는데 도움이 되는 feature는 무엇인지 가늠할 수 있습니다.
(2) 서로 다른 두 feature의 상관관계: 만약 두 feature가 매우 강한 상관 관계를 갖는다면, 두 변수 중 하나만 알아도 다른 변수의 값을 알 수 있기 때문에 하나만 선택해서 사용해야 합니다.
공분산
공분산은 두 변수의 상관관계를 측정할 수 있는 지표입니다. 두 변수 $X, Y$의 공분산을 계산하는 방법은 아래와 같습니다.
$Cov(X, Y) = E\left[(X-\mu_X)(Y-\mu_Y)\right]$
직관적으로, 각 변수의 _평균을 기준으로 한 데이터의 상대적인 위치_가 서로 비슷할수록 높은 상관관계를 갖는다고 볼 수 있습니다. 공분산은 아래의 성질을 갖습니다.
(1) $Cov(X, X) = Var(X)$
(2) $Cov(X, Y) = Cov(Y, X) $
공분산을 구할 때에도, 평균이 활용되므로 자유도는 $n-1$이 됩니다.
상관계수
공분산을 통해 두 변수 사이의 상관관계는 알 수 있지만, 두 변수의 단위가 다르므로, 공분산 값의 크기로 상관관계의 정도를 파악할 순 없습니다. 따라서 이를 가늠할 수 있도록 공분산 값을 [-1, 1] 사이의 값으로 조정할 필요가 있습니다.
상관계수(a.k.a 피어슨 상관계수)는 공분산 값을 두 변수의 표준편차의 곱으로 나눠서 그 값을 [-1, 1] 범위로 조정합니다. 식으로 표현하면 아래와 같습니다.
$Corr(X, Y) = \frac {Cov(X, Y)}{\sigma_X\sigma_Y}$
주의: 서로 독립인 두 변수의 공분산과 상관계수는 0이지만, 역은 성립하지 않습니다.
왜냐하면 앞서 설명한 상관관계는 두 변수 사이의 선형 관계만을 나타내기 때문입니다. 즉, 일차식으로 표현할 수 있는 범위에서의 상관관계를 알 수 있는 겁니다.
독립은 한 변수의 변화가 다른 변수의 변화에 영향을 끼치지 않는 것을 의미하므로, 두 변수가 선형 관계뿐만 아니라 다항식, 지수, log관계 등 어떤 관계도 갖지 않는 것을 의미합니다.
Python coding
지금까지 정리한 내용을 간단한 python 코드로 확인해보겠습니다. Practical Statistics for Data Scientists이란 책에서 상관관계를 시각화해주는 R코드 예시를 보여주는데, python으로 다시 짜 보겠습니다.
[code download], [data download]
import numpy as np
import pandas as pd
import seaborn as sns
# AT&T와 버라이즌의 일별 주식가격 등락률 정보 로드
save_path = "./img/2021-02-23"
sp500_px_df = pd.read_csv('data/sp500_data.csv') # S&P500에 있는 회사의 일별 주식 등락 정보
sp500_px_df.rename(columns={'Unnamed: 0': 'Dates'},inplace=True)
atnt = 'T' # AT&T 종목코드
verizon = 'VZ'# 버라이즌 종목코드
{% endhighlight %}
S&P500에 있는 AT&T와 버라이즌이라는 회사의 주가 등락률의 상관관계를 분석해보겠습니다. 유명한 기업들로 해보고 싶었는데, 상관계수가 작아서 시각화할 때 안 예뻐서 이 둘로 정했습니다!
# AT&T과 버라이즌의 공분산 계산
cov_av = np.cov(sp500_px_df[atnt], sp500_px_df[verizon])
print(cov_av) ''' [[0.08390944 0.05784096]
[0.05784096 0.10472254]]'''numpy의 cov() 함수를 사용하면 두 변수 사이의 공분산 행렬을 반환합니다.
(0, 0), (1, 1)은 각각 AT&T와 버라이즌의 분산을 의미하고, (0, 1), (1, 0)은 AT&T와 버라이즌의 공분산으로, 두 값은 같습니다.
Numpy를 이용해서 공분산을 계산할 때는 위의 수식과는 달리 자유도를 고려하지 않습니다. 자유도를 고려하기 위해서는 ddof변수를 1로 설정합니다.
# AT&T과 버라이즌의 상관계수 계산
corr_av = np.corrcoef(sp500_px_df[atnt], sp500_px_df[verizon])
print(corr_av) '''[[1. 0.61703529]
[0.61703529 1. ]]'''
`corrcoef()`함수를 사용하면 두 변수 사이의 상관계수 행렬을 반환합니다.<br>(0, 0), (1, 1)은 자신과의 상관계수 이므로 최대값인 1이고, (0, 1), (1, 0)은 AT&T와 버라이즌의 상관계수입니다. 두 회사는 꽤 높은 **양의 상관관계**를 갖는다고 볼 수 있습니다.
# scatterplot
ax = sns.scatterplot(data=sp500_px_df, x=atnt, y=verizon, color='r')
ax.axhline(0, color='grey', lw=1) # 수평선 추가
ax.axvline(0, color='grey', lw=1) # 수직선 추가
fig = ax.get_figure()
fig.savefig(f"{save_path}/scatter.png")
두 변수의 상관관계를 확인할 때 가장 많이 사용하는 scatterplot입니다. 한눈에 상관관계를 확인할 수 있습니다.
하지만 scatterplot은 데이터가 너무 많은 경우 점이 겹쳐 보이기 때문에, 겹쳐 보이는 부분의 밀도는 확인하기 어려운 한계가 있습니다.
# hexbinplot
ax = sns.jointplot(data=sp500_px_df, x=atnt, y=verizon, kind='hex', gridsize=30, color='r')
ax.savefig(f"{save_path}/hexbin.png")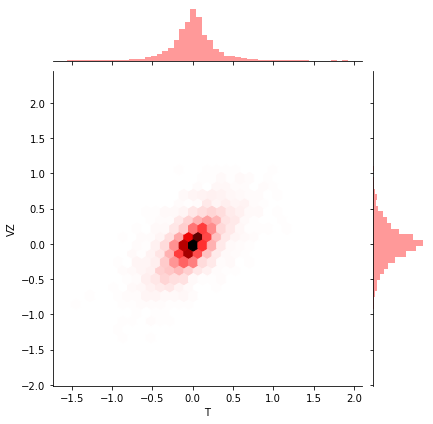
# contourplot
ax = sns.jointplot(data=sp500_px_df, x=atnt, y=verizon, kind='kde', color='r')
ax.savefig(f"{save_path}/contour.png")
위 두 자료는 scatterplot의 한계를 보완합니다. x좌표, y좌표 말고도 color성분을 추가해서 데이터 밀집 지역도 확인할 수 있습니다.
마무리
이 글에서는 상관관계와 공분산에 대해서 정리해봤습니다. 상관관계는 다양한 예측 변수를 활용해서 목표 변수를 예측하고자 할 때, 반드시 확인해봐야 합니다.
게시글 하나 만드는데 시간이 오래 걸리네요,,, 다른 분들은 어떻게 하시는지 ㅎㅎ
다음에는 다양한 확률 분포들 중, 이산형 확률분포에 대해서 정리하겠습니다.
긴 글 읽어주셔서 감사합니다! 좋은 하루 보내세요 :)
References
'[Mathmatics]' 카테고리의 다른 글
| [Statistics] 포아송과 친구들 (0) | 2021.04.27 |
|---|---|
| [Statistics] 이산형 확률분포 (0) | 2021.04.27 |
| [Statistics] 평균, 분산, 표준편차 (0) | 2021.04.27 |
| [Linear algebra] SVD (0) | 2021.04.27 |
| [Linear algebra] 주요 개념 및 성질(2) (0) | 2021.04.27 |