TwoPark

Intro

안녕하세요. 이번에는 vector의 tuple요소로 sort하는 방법에 대해 포스팅 하겠습니다.

vector의 tuple값으로 sort

프로그램을 하다 보면 vector에 tuple로 묶어서 데이터를 저장할 때 sort방법입니다.

#include <iostream>
#include <vector>
#include <algorithm>
#include <tuple>
using namespace std;
static bool CmpName(tuple<string, string, int> &v1, tuple<string, string, int> &v2)
{
    return get<0>(v1) > get<0>(v2);
}

int main(void)
{
    std::vector<tuple <string, string, int>> v;
    v.push_back(make_tuple("workid 1", "2021-10-27 08:20:18", 3));
    v.push_back(make_tuple("workid 2", "2021-10-28 09:22:18", 5));
    v.push_back(make_tuple("workid 3", "2021-10-29 10:18:18", 7));
    v.push_back(make_tuple("workid 5", "2021-10-27 14:32:18", 1));
    v.push_back(make_tuple("workid 8", "2021-10-27 14:47:18", 2));
    v.push_back(make_tuple("workid 6", "2021-10-30 14:36:18", 6));
    v.push_back(make_tuple("workid 4", "2021-10-29 11:12:18", 4));
    v.push_back(make_tuple("workid 9", "2021-10-26 08:20:18", 8));
    v.push_back(make_tuple("workid 7", "2021-10-27 14:37:18", 5));

    sort(v.begin(), v.end());
    for (int i = 0; i < v.size(); i++)
        cout << get<0>(v[i]) << "\t" << get<1>(v[i]) << "\t" << get<2>(v[i]) << endl;
        return 0;
}

결과

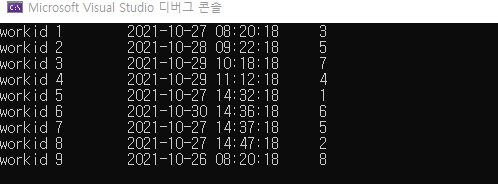
일반적으로 sort를 하면 tuple의 첫번째 값에 의해 오름차순 sort가 됩니다. 하지만 제가 원하는건 tuple의 다른 요소로 sort하는 방법입니다.

#include <iostream>
#include <vector>
#include <algorithm>
#include <tuple>
using namespace std;

static bool CmpName(tuple<string, string, int> &v1, tuple<string, string, int> &v2)
{

    return get<2>(v1) < get<2>(v2);//tuple 3번째 값으로 비교

}

int main(void)
{
    std::vector<tuple <string, string, int>> v;

    v.push_back(make_tuple("workid 1", "2021-10-27 08:20:18", 3));
    v.push_back(make_tuple("workid 2", "2021-10-28 09:22:18", 5));
    v.push_back(make_tuple("workid 3", "2021-10-29 10:18:18", 7));
    v.push_back(make_tuple("workid 5", "2021-10-27 14:32:18", 1));
    v.push_back(make_tuple("workid 8", "2021-10-27 14:47:18", 2));
    v.push_back(make_tuple("workid 6", "2021-10-30 14:36:18", 6));
    v.push_back(make_tuple("workid 4", "2021-10-29 11:12:18", 4));
    v.push_back(make_tuple("workid 9", "2021-10-26 08:20:18", 8));
    v.push_back(make_tuple("workid 7", "2021-10-27 14:37:18", 5));

    sort(v.begin(), v.end(), CmpName);
    for (int i = 0; i < v.size(); i++)
        cout << get<0>(v[i]) << "\t" << get<1>(v[i]) << "\t" << get<2>(v[i]) << endl;
        return 0;
}

결과

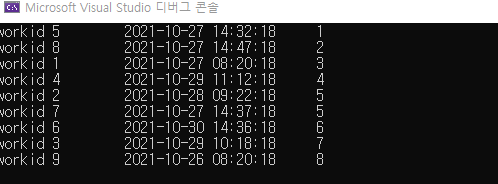
sort에 CmpName를 추가 하여 tuple의 3번째 값으로 오름 차순 정렬을 했습니다. 내림차순은 CmpName함수에서 return get<2>(v1) < get<2>(v2); 값을 return get<2>(v1) > get<2>(v2); 부등호를 바꿔 주면 됩니다.

마무리

이상으로 포스터를 마치겠습니다. 요즘 회사에서 바빠서 포스팅을 많이 올리지 못했는데 자주 올리도록 노력해 보겠습니다.

감사합니다.

Intro

안녕하세요. 이번에는 for문에서 vector.erase()를 사용하는 방법에 대해 포스팅 하겠습니다.

for문에서 Vector erase 사용하기

vector에 1, 3, 2, 1,1, 3, 2, 1,1, 3, 2, 1 를 넣고 값이 1인 값의 인덱스를 erase를 통해 삭제 해보도록 하겠습니다.

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    vector <int> v;
    v.push_back(1);
    v.push_back(3);
    v.push_back(2);
    v.push_back(4);
    v.push_back(1);
    v.push_back(3);
    v.push_back(2);
    v.push_back(4);
    v.push_back(1);
    v.push_back(3);
    v.push_back(2);
    v.push_back(4);

    cout << "Vector 값 출력 -----------------------" << endl;
    for (int i = 0; i < v.size(); i++)
        cout << v[i] << endl;

    for (int i = 0; i < v.size(); i++) //vector에서 값이 1인 값을 삭제
        if (v[i] == 1)
            v.erase(v.begin(), v.begin()+i);

    cout << "일반 for문 erase vector 출력-----------------------" << endl;
    for (int i = 0; i < v.size(); i++)
        cout << v[i] << endl;
}

결과

결과를 보고 엇? 뭐지 이러실수 있습니다. 제가 지우고 싶은 값은 vector의 값이 1인 index인데 결과를 보면 값이 1인 index가 전부 지워지지 않았습니다.
왜냐하면 일반적인 증감 for문에 vector.erase를 사용하면 정상적으로 작동하지 않습니다. erase함수는 해당 요소를 지운 후 지워진 요소 뒤의 요소를 가르키기 떄문입니다. 따라서, for문을 돌면서 erase를 통해 index의 vector의 값을 삭제하면서도 계속 for문에서 i값을 증감을 계속 하기 때문입니다. 그렇기 때문에 erase를 하지 않았을 때 i값을 증감시켜야 원하는 결과를 얻을 수 있습니다.

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    vector <int> v;
    v.push_back(1);
    v.push_back(3);
    v.push_back(2);
    v.push_back(1);
    v.push_back(1);
    v.push_back(3);
    v.push_back(2);
    v.push_back(1);
    v.push_back(1);
    v.push_back(3);
    v.push_back(2);
    v.push_back(1);

    cout << "Vector 값 출력 -----------------------" << endl;
    for (int i = 0; i < v.size(); i++)
        cout << v[i] << endl;

    for (int i = 0; i < v.size();)
        if (v[i] == 1)
            v.erase(v.begin() + i);
        else
            i++;


    cout << "erase vector 출력-----------------------" << endl;
    for (int i = 0; i < v.size(); i++)
        cout << v[i] << endl;
}

for문 안에 i값을 증감하지 않고 erase를 하지 않았을 때 i값을 증감하면 원하는 결과를 얻을 수 있습니다.

마무리

이상으로 포스터를 마치겠습니다. 다음번에는 vector의 sort에 대해 알아보도록 하겠습니다.

Intro

안녕하세요, 지난 글에서는 소개한 HNE(Heterogeneous Network Embedding) Proximity-Preserving methods 중 random walk based approaches에 대해서 정리했는데요, 오늘은 이어서 First/Second-Order Proximity Based Approaches에 대해서 정리하겠습니다.

이번 글 역시 heterogeneous network representation learning a unified framework with survey and benchmark 논문의 내용을 정리합니다.

First/Second-Order Proximity based approaches는 비교적 간단해서, First/Second-Order Proximity based approaches에 대해서 정리한 뒤 Proximity-Preserving methods에 대한 부가적인 내용을 추가해서 정리하겠습니다.

한글표현과 영어표현이 아래와 같이 섞여서 사용될 수 있습니다

그래프, 네트워크: graph, network (두 단어는 interchangeable)
객체: node
연결: edge

Random walk based approaches vs. First/Second-Order Proximity based approaches

Random walk based approaches와 First/Second-Order Proximity Based Approaches의 차이는 무엇일까요? 제 주관적인 의견을 적어보겠습니다.

Random walk based approaches는 주로 source node로 부터 random walk를 수행해서 주어진 meta path의 모양을 갖는 path들을 찾았는데요, 이를 이용하면 여러 hop 떨어진 node사이의 관계도 고려할 수 있게 됩니다. 하지만 random walk를 수행하는 임의성이 있기 때문에, source node와 1 hop관계를 갖는 node라 할 지 라도 선택받지 못할 수 있습니다.

반면에 First/Second-Order Proximity Based Approaches의 경우에는 이름에도 적혀있듯이, 각 source node의 1 or 2 hop 관계의 모든 node를 고려합니다. 대신 이 경우 Random walk based approaches와 달리 여러 hop (>2) 관계에 있는 node들의 관계는 학습에 사용되지 않습니다.

그래서 저는 데이터만 충분하다면 여러 hop을 고려할 수 있는 random walk based 기반 방법이 더 좋지 않을까? 생각합니다.

HNE는 아니지만 개인적인 프로젝트에서 random walk based approach인 Deepwalk와 first/second-order proximity based approach인 LINE을 사용했을 때, Deepwalk이 더 좋은 성능을 보였던 경험이 있기도 합니다.

First/Second-Order Proximity based approaches

PTE

PTE는 Predictive Text Embedding의 약자로, NLP분야에서 사용되는 HNE기법입니다. PTE는 여러 개의 edge type $l \in L$이 있을 때, 각 edge type만으로 이루어진 sub graph (bipartite graph)를 만든 뒤에 각 graph별로 node embedding을 최적화합니다. objective는 아래와 같습니다.

$$\mathcal{J}=\sum_{l \in L}\sum_{u, v\in V}w_{uv}^l\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V_{\phi(u)}}exp(e_{u^{'}}^{T}e_{v})}$$

$w_{uv}^l$은 type이 $l$인 edge로 연결된 node $u, v$사이의 weight입니다. 연결이 있으면 0이상의 값이, 없으면 0을 갖습니다. $V_{\phi(u)}$는 $u$와 같은 type인 node의 집합입니다. 그리고 위 objective는 결국 edge type에 대해서 aggregation이 가능해서, 아래와 같이 변형가능합니다.

$$\mathcal{J}=\sum_{u, v\in V}w_{uv}\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V_{\phi(u)}}exp(e_{u^{'}}^{T}e_{v})}, w_{uv}=\sum_{l}w_{uv}^l$$

이처럼 PTE는 다소 간단한 방법이라고 볼 수 있습니다.

AspEm

AspEm는 PTE에서 한단계 발전한 모델입니다. 각 edge type별로 sub graph를 만들었던 PTE와 달리, 사전에 정의된 Aspect에 해당하는 edge type들로 이루어진 sub graph를 만들고, 이들을 각각 최적화합니다.

여기서 aspect는 사용자가 정의하기 나름인데요, 예를들어 영화 dataset인 IMDB dataset으로 만든 HN이 user, movie, actor, director, genre 5가지 edge type으로 이루어져 있다고 하겠습니다. 그러면 여기서 user가 좋아하는 actor를 위주로 embedding을 수행하고 싶다면, 우리는 node로는 user, movie, actor node type인 node를 갖고, edge는 user-movie, movie-actor를 잇는 edge type만으로 이루어진 sub graph를 추출해서 이를 최적화하면 됩니다.

edge type의 집합 $L$이 있을 때, 이것의 부분 집합으로 한 aspect $a$에 대한 edge type의 집합은 $L^a \subseteq L$입니다.

따라서 각 aspect $a$에 대한 sub graph의 embedding 최적화는 아래 objective에 따라 이루어 집니다.

$$\mathcal{J}=\sum_{l \in L^a}\frac{1}{Z_l}\sum_{u, v\in V}w_{uv}^l\log\frac{exp(e_{u, a}^{T}e_{v, a})}{\sum_{u^{'}\in V_{\phi(u)}}exp(e_{u^{'},a}^{T}e_{v,a})}$$

HEER

Heterogeneous information network Embedding via Edge Representations의 약자입니다 ㅋㅋ 되게 기네요.

HEER 역시 PTE의 변형으로, edge type별 embedding도 함께 학습하는 특징이 있습니다. objective는 아래와 같습니다.

$$\mathcal{J}=\sum_{l \in L}\sum_{u, v\in V}w_{uv}^l\log\frac{exp(\mu_l^Tg_{uv})}{\sum_{u^{'}, v^{'}\in P_l(u, v)} exp(\mu_l^Tg_{u^{'}v^{'}})}$$

$\mu_l$은 edge type $l$의 embedding이고, $g_{uv}$는 node $u, v$의 edge embedding으로 $g_{uv}=e_u \odot e_v$ 입니다. ($\odot$: element wise product)

이때, $\mu_l$의 원소를 대각성분으로 갖는 diagonal matrix $A_l$을 사용해서 아래와 같은 bilinear form으로 변형할 수 있게 됩니다.

$$\mathcal{J}=\sum_{l \in L}\sum_{u, v\in V}w_{uv}^l\log\frac{exp(e_u^T A_l e_v)}{\sum_{u^{'}, v^{'}\in P_l(u, v)} exp(e_{u^{'}}^T A_l e_{v^{'}})}$$

그 외

위에서 설명한 3가지 모델을 포함해서 나머지 First/Second-Order Proximity based approaches를 정리한 표를 논문에서 인용해서 첨부하겠습니다.

Network Smoothness Enforcement

여기까지 Proximity-Preserving methods에 대해서 대략적인 정리를 해봤습니다. 논문의 저자들은 흥미로운 insight를 제시했는데요, 우선 여러 모델의 objective는 아래와 같이 일반화 할 수 있습니다.

$$max \mathcal{J}=\sum_{u, v\in V}w_{uv}\log\frac{s(u, v)}{\sum_{u^{'}}s(u', v)} + \mathcal{J}_{R_0}$$

$s(u, v)$는 node $u, v$의 유사도를 나타내는 함수로, $f(e_u)^Tf(e_v)$로 나타낼 수 있습니다. 대부분의 method는 $f$를 항등 함수로 사용하겠지만, HIN2Vec는 $f(e_u)=\sqrt{M}e_u$, HEER은 $f(e_u)=\sqrt{A_l}e_u$이 될 수 있습니다. (왜 bilinear form으로 변형했는지 알 수 있는 대목입니다!)

위 식을 negative sampling 형태로 변환 한뒤, 정리를 하면, $\mathcal{J}_{R_0}$외에 2가지 regulization term을 발견할 수 있습니다.

마지막 수식을 보면, 결국 대부분의 HNE 모델의 objective는 1) 두 node $u, v$의 embedding이 유사해지고 (빨간 박스 첫번째 줄), 2) $u, v$의 embedding의 크기가 0보다 커지게 하고, (빨간 박스 두번째 줄) 3) $u$가 아닌 나머지 $u^{'}$에 대해서는 v와 유사해지지 않도록 (빨간 박스 세번째 줄) 최적화가 됩니다.

1)은 objective의 주 목적이고, 2)는 $u, v$의 embedding이 모두 zero vector 되지 않도록 하고, 3)은 모든 node의 embedding이 동일해지지 않도록 하는 역할을 하게 됩니다.

단순히 수식만 재배열 했을 뿐인데 이런 insight을 얻을 수 있네요.

마무리

오늘은 여러 First/Second-Order Proximity based approaches를 정리하고, 대부분의 HNE 모델들이 갖는 objective에 대한 insight을 정리해봤습니다.

사실 proximity-preserving 모델들은 shallow하다고 볼 수 있습니다. 최적화학 모델의 layer가 1개만 있는 거죠. 그러다 보니 non-linearity가 부족한 특징이 있습니다.

다음에는 조금 더 deep한 모델들을 사용하는, Message-passing methods에 대해서 정리하겠습니다.

감사합니다!

References

Heterogeneous Network Representation Learning: A Unified Framework with Survey and Benchmark
PTE: Predictive Text Embedding through Large-scale Heterogeneous Text Networks
ASPEM: Embedding Learning by Aspects in Heterogeneous Information Networks
Easing Embedding Learning by Comprehensive Transcription of Heterogeneous Information Networks

Intro

안녕하세요, 오늘은 지난 글에서 소개한 HNE(Heterogeneous Network Embedding) 에 중에서 Proximity-Preserving methods에 대해서 정리해보겠습니다.

proximity는 무엇일까요? 사전 상의 의미는 _가까움_입니다. 그래프 임베딩은 그래프의 목적은 topological information (위치, 연결 정보)을 보존하는 것이라고 말씀드렸죠? 그런 의미에서 Proximity-Preserving methods를 해석하면 실제 그래프 상에서 node들이 가까운 정도를 보존하면서 임베딩을 수행하는 방법들이라고 할 수 있고, 이는 topological information을 보존하는 하나의 방법으로 볼 수 있습니다. 그 외에 방법들에 대해서는 다음 글에서 정리하도록 하겠습니다.

이번 글 역시 heterogeneous network representation learning a unified framework with survey and benchmark 논문의 내용을 정리합니다.

논문에서 설명하는 Proximity-Perseving methods는 크게 random walk based approaches와 first/second order proximity based approaches가 있습니다. 오늘은 이 두 접근법들 중 random walk baed approaches에 대해서 정리해보겠습니다.

한글표현과 영어표현이 아래와 같이 섞여서 사용될 수 있습니다

그래프, 네트워크: graph, network (두 단어는 interchangeable)
객체: node
연결: edge

Random walk based approaches

Metapath

Random walk based approaches를 이해하기 위해서는 meta path라는 것에 대해서 알 필요가 있습니다. HN (Heterogeneous Network)는 여러 type의 node와 edge로 구성된 복잡한 그래프 입니다. 이 그래프 상의 임의의 node $n_0$ 에서 연결된 edge를 따라 $m-1$번 이동해서 다른 node $n_m$에 도착했다고 가정해보죠. 그러면 아래와 같은 path가 생성될 겁니다.

$$n_0 \xrightarrow{e_1} n_1 \xrightarrow{e_2} \dots \xrightarrow{e_{m-1}} n_{m-1} \xrightarrow{e_m} n_m$$

여기서, $k$번째 node의 type을 $o_k$, edge의 type을 $l_k$로 하겠습니다. 그러면 위의 path는 다시 아래와 같이 표현이 가능해지죠

$$o_0 \xrightarrow{l_1} o_1 \xrightarrow{l_2} \dots \xrightarrow{l_{m-1}} o_{m-1} \xrightarrow{l_m} o_m$$

바로 위와 같이 표현된 node와 edge의 type을 만족하는 path들을 meta path라고 합니다. 각각의 $o_k, l_k$에는 같은 type의 node, edge라면 무엇이든 올 수 있습니다. (물론 실제로 edge로 이어진 것들만 가능합니다.)

metapath2vec

이제 Random walk based approach중 하나인 metapath2vec에 대해서 이해할 준비가 되었습니다.

사전에 정의된

metapath $$M=o_0 \xrightarrow{l_1} o_1 \xrightarrow{l_2} \dots \xrightarrow{l_{m-1}} o_{m-1} \xrightarrow{l_m} o_m$$이 있습니다.

이제 HN상의 모든 node $v\in V$에 대해서, 위 $M$의 형태를 갖는 metapath를 생성해내는 겁니다. node당 몇 개의 metapath를 만들지는 hyperparameter로 설정할 수 있습니다. 이러한 방법의 조상 격 방법인 DeepWalk의 경우 node당 10개의 metapath를 생성했습니다.

경우에 따라서 한 node로 부터 만들 수 있는 ($M$의 형태를 만족하는) path는 매우 많아질 수 있기 때문에, 우리는 random walk를 통해서 수많은 가능한 path 중 10개 정도를 뽑습니다.
만약 type이 $o_{i-1}$인 $i-1$번째 node $n_{i-1}$에서 type이 $o_i$인 $i$번째 node $n_i$를 결정할 때, $n_{i-1}$과 edge type이 $l_i$인 edge로 연결된 여러 node들 $N_{n_{i-1}}^{l_{i}}$이 있으면, $\frac{1}{|N_{n_{i-1}}^{l_{i}}|}$의 확률로 하나를 선택하게 됩니다.

자 그럼 이제 이렇게 해서 각 node $v\in V$별로 $M$의 형태를 갖는 여러 path들인 $P={P_1, P_2, \dots, P_{K}}, (K=|V| \times 10)$를 얻었습니다. 그럼 우리는 이제 얻은 path에 있는 node들의 embedding을 아래 objective function을 따라서 최적화하게 됩니다.

$$\mathcal{J}=\sum_{v\in V}\sum_{u\in \mathcal{C(v)}}\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})}$$

$C(v)$는 node $v$의 context입니다. context는 random walk로 생성한 path $P_k \in P$에서, 대상 node의 앞, 뒤에 존재하는 node들을 의미합니다. 이 또한 앞, 뒤로 몇 개씩의 node를 context로 볼 지는 hyperparameter로 설정할 수 있으며, 그 크기를 _window size_라고합니다. window size가 2라면, 생성한 path에서 대상 node의 앞, 뒤로 2개씩 총 4개의 node를 context로 보겠다는 뜻입니다.

위 objective상에서는 각 node별로 context에 대해서 최적화한다고 표현이 되어있지만, 실제 구현할 때는 만들어진 path를 stride하면서 기준 node와 그 앞 뒤 node들을 context로 보고 최적화하지 않을까 예상됩니다.

위의 objective는 최대화해야하는 대상으로, 생성한 path상에 존재하는 각 node에 대해서 그 node와 그 node의 context node들의 embedding dot product가 모든 non-context node들에 대한 dot product의 합에 대해서 높은 비율을 갖도록하는 것이 목표입니다.

metapath2vec은 여기서 한 가지 variant를 더 만드는 데요, 바로 대상 node $v$의 context $C(v)$에서 여러 번 발견되는 context node $u$에는 더 큰 weight $W_{vu}$를 부여하는 것 입니다.

$$\mathcal{J}=\sum_{v\in V}\sum_{u\in \mathcal{C(v)}}w_{vu}\log\frac{exp(e_{u}^{T}e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})}$$

마지막으로, 위 objective를 더 빠르게 최적화 할 수 있는 방법도 있습니다. negative sampling이라는 방법인데요, 비단 metapath2vec 뿐만 아니라 위 objective처럼 softmax형태를 띄는 objective를 최적화 할 때 많이 대체되는 방법입니다. 위 objective에서, 분모부분인 $\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}e_{v})$의 계산은 expensive하기 때문에, 모든 node를 고려하지 않고 이를 approximate할 수 있는 방법인 negative sampling을 사용합니다.

HIN2Vec

이 논문에서는 HN을 HIN(Heterogeneous Information Network)라고 표현했습니다.

HIN2Vec이 최적화 하려고 하는 parameters는 3개의 embedding matrix $W_X, W_Y, W_R$입니다. $W_X, W_Y \in R^{|V| \times d}$는 source node embedding과 target node embedding이고, $W_R \in R^{|L| \times d}$는 고려하고자 하는 모든 $M$의 각 embedding입니다. ($|L|$은 고려하고자 하는 모든 $M$의 종류 수)

node $u, v$의 embedding은 각각 $e_u = W_X^u, e_v = W_Y^v$, 그리고 $M$의 embedding은 $e_r = f_{01}(W_R^M), f_{01}(.) = normalize func.$가 됩니다.

HIN2Vec은 학습을 위해서 random walk를 통해 positive tuple인 $(u, v, M)$을 찾습니다. node $u$와 $v$가 meta-path $M$을 통해 연결되어있다는 걸 뜻합니다. 그리고 여러 개의 random node $u^{'}$와 함께 아래의 objective를 최적화합니다.

$$\mathcal{J}=\sum_{(u, v, M)}\log{p(M|u, v)} + \sum_{(u^{'}, v, M)}\log{(1 - p(M|u^{'}, v))}$$
$$=\sum_{(u, v, M)}\left(\log{\sigma(e_u^T A_M e_v)} + \sum_{u^{'}}\log{\sigma(-e_{u^{'}}^T A_M e_v)}\right)$$

$A_M$은 $e_r$의 값으로 만든 diagonal matrix입니다. 위의 object 또한 negative sampling 형식이며 아래의 softmax값을 approximate합니다.

$$\mathcal{J}=\sum_{M}\sum_{(u, v)\in V}w_{uv}^M\log\frac{exp(e_{u}^{T} A_M e_{v})}{\sum_{u^{'}\in V}exp(e_{u^{'}}^{T}A_M e_{v})}$$

마무리

오늘 정리한 metapath2vec, HIN2Vec말고도 여러 random walk 기반의 proximity-preserving methods가 있습니다. 논문에 첨부된 표를 인용하면서 이번 글 마치겠습니다!

감사합니다.

References

Heterogeneous Network Representation Learning: A Unified Framework with Survey and Benchmark
metapath2vec: Scalable Representation Learning for Heterogeneous Networks
HIN2Vec: Explore Meta-paths in Heterogeneous Information Networks for Representation Learning

Intro

안녕하세요, 오늘은 머신 러닝 알고리즘의 한 종류인 HNE(Heterogeneous Network Embedding) 에 대해서 정리해보겠습니다.

네트워크, 그래프라고 알려져 있는 자료구조는 여러 객체 사이의 관계를 표현하는데 매우 효과적입니다.

어떤 객체와 직접/ 간접적으로 연결되어있는 객체들을 분석하면 우리는 이 객체와 유사한 객체들을 찾을 수 있습니다.

하지만 문제가 있습니다. 직접/ 간접적인 연결이 너무 많다는 겁니다. 이는 우리가 일일이 다 고려할 수 없는 수준이죠.

어떤 객체는 10개의 다른 객체와 연결되어 있는 반면, 어떤 객체는 10,000개의 다른 객체와 연결되어있기도 합니다. 간접적인 연결까지 다 고려하면 이루 말할 수 없는 다양한 연결 관계가 존재합니다.

따라서 그래프 (또는 네트워크)는 그동안 다루기 어려운 자료구조로 여겨져 왔습니다. 이 복잡한 관계를 분석하려면 많은 연산이 필요하니까요!

하지만 머신 러닝 기술이 발전하고 하드웨어 스펙이 좋아지면서, 이 까다로운 자료구조를 다룰 수 있는 기술이 등장합니다.

바로 그래프 임베딩 (Graph Embedding) 입니다.

저는 그래프 임베딩 중에서도, 그래프를 구성하는 node와 edge의 종류가 여러 개인 Heterogeneous network (graph) embedding 에 대해서 공부해서 정리하려고 합니다.

heterogeneous network representation learning a unified framework with survey and benchmark 라는 논문의 내용을 정리할 거고, 내용이 많아서 여러 개에 나눠서 하려고 합니다.

한글표현과 영어표현이 섞여서 사용될 수 있습니다. 아래 단어 사전을 참고하세요.

• 그래프, 네트워크: graph, network (두 단어는 구분없이 사용됩니다.)
• 객체: node
• 연결: edge

Graph Embedding

그래프 임베딩은 그래프를 구성하는 객체들을 낮은 차원의 벡터로 표현하는 기술입니다.

$N$개의 객체 (node)로 이루어진 그래프를 있는 그대로 표현하려면, 적어도 $N \times N$크기의 인접 매트릭스가 필요합니다. 그래서 어느 두 객체가 연결되어 있으면 (edge가 존재하면) 해당 부분은 1, 아니면 0으로 채워지게 되는 것이죠. 물론 edge에 가중치 (weight)가 있거나, edge에 방향이 있는지 (directed), 없는지 (undirected)에 따라서 달라집니다.

그리고 이 인접 매트릭스는 매우 sparse하기 때문에 (대부분이 0이기 때문에), 낭비되는 메모리도 크고, 많은 연산량을 필요로 합니다. 그리고 직접적인 연결 정보만을 알 수 있죠. 이 인접 매트릭스만으로는 그래프의 직접/ 간접적인 풍부한 연결정보를 모두 파악하기 어렵습니다.

하지만 그래프 임베딩 기술을 적용한다면, $N \times d,, (d << N)$인 매트릭스의 각 값에, 다른 객체들 사이의 직접/ 간접적인 연결 정보를 고려한 값을 채울 수 있습니다. 각 객체는 $d$차원의 벡터로 표현이 되는데, 이때 그래프 상에서의 구조적 정보 (topological information)을 보존하는 형태로 표현이 됩니다. 그래프 상에서 가까우면, 비슷한 벡터로 표현이 된다는 뜻 입니다.

이렇게 그래프를 구성하는 각 node가 표현된 $d$차원 벡터를 latent vector, 또는 node의 representation이라고 합니다. 그래프 임베딩은 이 latent vector를 어떻게 구하느냐에 따라 여러 방법이 존재합니다.

수식으로 표현하면 $${\Phi}: V \rightarrow \mathcal{R}^{|V|\times d}$$

그래프 임베딩의 가장 시초격인 방법은 DeepWalk입니다. 그래프 임베딩에 관심이 있으신 분이라면 꼭 논문을 읽어보시길 추천드립니다.

HNE (Heterogeneous Network Embedding)

Intro에서 잠깐 말씀드렸듯이, heterogeneous network는 그래프를 구성하는 node와 edge의 종류가 여러개인 그래프입니다. 조금 더 복잡하지만, 더 풍부한 표현이 가능합니다. 구글에서 사용한다고 알려진 지식 그래프 (knowledge graph) 도 heterogeneous graph의 한 종류 입니다.

HNE를 위해서는 node의 type을 고려해야 합니다. 따라서 수식이 아래와 같이 달라집니다.

$${\Phi}_k: V_k \rightarrow \mathcal{R}^{|V_k|\times d}$$

여기서 $k$는 여러 개의 node type 중 $k$번째 type을 의미합니다. 이런식으로 HNE는 각 type의 node들의 latent vector를 학습하는 방법입니다.

마무리

오늘은 그래프 임베딩은 무엇인지, 그리고 HNE는 또 무엇인지 정리해봤습니다.

사실 그래프 임베딩은 node 뿐만 아니라 edge를 임베딩할 수도 있고, 그래프 전체를 embedding할 수 있습니다. 하지만 대부분의 경우 node embedding을 목표로 합니다.

다음 글에서는 조금 더 자세히, HNE는 어떤 방법들이 있는지 정리하겠습니다.

감사합니다!

Intro

안녕하세요, 오늘은 MLE(Maximum Likelihood Estimation) 에 대해서 정리하겠습니다.

MLE는 많은 머신 러닝, 특히 deep learning에서 자주 등장하는, 꼭 알아야할 개념 중 하나입니다.

Likelihood

Likelihood는 우리말로 가능도, 또는 우도라고 합니다.

영어 표현에 *"be likely to -" (- 할 것 같은)* 이라는 숙어가 있잖아요? 따라서 likelihood 또한 비슷한 느낌으로 *"~ 할 것 같은 정도"* 로 받아들일 수 있을 거 같습니다.

그리고 이는 통계학의 관점에서 풀어보면, 어떤 고정된 파라미터 $\theta$를 갖는 분포가 있을 때, 이 분포에서 특정 sample (또는 event) $x$가 발견(또는 수집)될 거 같은 정도로 할 수 있습니다.

수식으로 표현해보자면 아래와 같습니다.

한 개의 sample $x$에 대해서는 $p(x|\theta)$

$n$ 개의 sample set $X = {x_1, x_2, \dots, x_n}$에 대해서는 $\prod_{i=1}^n p(x_i|\theta)$

편의를 위해 둘 다 $P(X|\theta)$라고 하겠습니다.

여기서 우리가 관심을 가져야할 변수는 바로 $\theta$ 입니다. 이 $\theta$는 우리가 사용하는 모델이 gaussian distribution이라면 평균 $\mu$와 분산 $\sigma$가 될테고, deep learning 모델이라면 이 모델이 갖고있는 모든 파라미터가 될 것입니다.

Maximum Likelihood Estimation

Likelihood의 느낌을 어느정도 잡으셨다면 MLE는 말 그대로 likelihood를 최대화 해주는 파라미터 $\theta$를 예측하는 일입니다. 즉, $\theta$가 어떤 값을 가져야 발견(또는 수집) 된 sample (또는 event)들이 발생할 확률이 최대가 될까? 에 대한 답을 찾는 것입니다.

수식으로는 $\hat{\theta} = argmax P(X|\theta)$로 표현할 수 있습니다.

간단하게 동전 던지기로 예시를 들겠습니다.

동전은 앞면과 뒷면 단 두개의 값만 가질 수 있고, 여러 번 동전 던지기를 수행했을 때 각 동전 던지기의 결과를 x라고할 수 있습니다. 그리고 우리가 관심있어하는 파라미터 $\theta$는 이 문제의 경우 "앞면이 나올 확률" 1개 입니다.

그렇다면 이를 MLE관점에서 보자면 우리가 알고싶은 것은 $n$번의 동전 던지기를 수행해서 앞면이 $k$번, 뒷면이 $n-k$번 나왔을 때, 이 결과가 나올 확률을 최대로 만들어 주는 파라미터 $\theta$는 무엇인가? 입니다.

위 예시와 관련한 구체적인 설명은 이 글을 참고해주세요.

Why MLE?

MLE문제를 푸는 것은 deep learning 모델을 최적화하는 문제와 많이 유사합니다.

대표적인 지도학습 예시인 classification을 생각해보겠습니다.

파라미터 $\theta$를 갖는 모델 $f$가 있을 때, 우리는 이 모델에게 어떤 sample을 주고, 이 sample의 class는 무엇인지 에측하도록 합니다.

예측을 하는 모델의 파라미터는 sample을 받기 전에 이미 정해져 있고 (given $\theta$), sample이 주어졌을 때 이 sample의 class가 무엇인지 값을 내놓습니다 ($f(x|\theta)$).

그리고 sample의 실제 class와 비교해서 그 차이에 따라 $\theta$를 최적화해나가죠.

이러한 관점에서 보았을 때, MLE는 deep learning에서 많이 쓰이는 개념 중 하나인 것입니다.

마무리

오늘은 MLE, Maximum Likelihood Estimation에 대해서 알아봤습니다.

MLE의 개념을 아는 것 만으로는 부족하고, 여러 모델이나 논문을 학습하면서 MLE의 개념이 어떻게 녹아들어 있는지 확인하면 좋을 거 같습니다.

References

데이터 사이언스 스쿨
Dive into Deep Learning

Intro

안녕하세요.
유닛 테스트는 무엇이길래 많은 개발자들이 중요성에 얘기 할까요?

유닛 테스트는 소프트웨어 개발자라면 한 번쯤은 들어 봤을 개념입니다. 많은 개발자들이 중요성은 인지하고 있지만 귀찮고 시간이 걸리기 때문에 안 하는 경우가 많습니다. 제가 이전에 다니던 회사에서도 유닛 테스트에 대한 말이 많았습니다. 왜 굳이 시간 들여서 하냐는 의견과 애당초 버그 없이 만들면 되는 거 아니냐는 의견이 있었습니다. 하지만 유닛 테스트는 분명 귀찮고 시간이 걸리는 것처럼 보이지만 실제로 효율적으로 사용한다면 오히려 개발할 때 생기는 디버깅 시간을 단축시 켬으로써 효율적인 프로그래밍이 가능합니다. 그리고 유닛 테스트는 프로그램 배포 전에 개발자가 검증할 수 있는 최소한의 도구라고 생각합니다. 제 고객이 테스터가 될 수는 없잖아요...

그러면 유닛 테스트에 대해 알아보도록 하겠습니다.

유닛 테스트란?

유닛 테스트는 컴퓨터 프로그래밍에서 소스 코드를 가장 작은 단위(함수 단위)로 나누어 의도된 대로 정확히 동작하는지 검증하는 테스트 메서드입니다.

유닛 테스트의 장점

1. 디버깅이 쉽다. 유닛 테스트의 목적은 프로그램을 작은 단위로 쪼개여 버그를 빠르게 파악하고, 버그 위치를 재빨리 찾아 빠른 디버깅이 가능합니다. 유닛 테스트를 하는 게 시간이 더 든다고 생각할 수 있겠지만 개발 기간 중 많은 시간을 할애하는 디버깅 시간을 단축시킴으로 여유 있는 프로그래밍이 가능하게 합니다.
2. 변경이 쉽다. 유닛 테스트 테스트 케이스가 잘 짜여 있으면, 내가 소스코드를 변경했을 때 유닛 테스트를 믿고 언제든지 리팩터링이 가능합니다. 리팩토링 후 해당 변경 내용이 의도대로 작동하는지는 유닛 테스트로 확인이 가능합니다. 또한, 유닛 테스트는 작성한 코드가 개발자의 의도대로 작동하는지 검증의 절차도 있지만, 코드 변경에 의한 사이드 이펙트를 최소화할 수 있습니다.
3. 통합이 간단하다. 유닛 테스트는 유닛 자체의 불확실성을 제가 해주기 때문에 상향식 테스트 방식에 유용합니다. 프로그램의 각 가분을 검증하고 그 부분을 다시 합쳐 다시 검증하는 통합 테스트에서 더욱 빛을 발휘합니다.
4. 코드 파악 쉽습니다. 테스트 케이스를 작성하다 보면 제가 만든 코드를 분석하며 어디에 영향이 끼치는지 파악이 가능하고 작성한 코드의 이해가 높아집니다.

훌륭한 단위 테스트란?
F. I. R. S. T

• Fast : 완성도 높은 프로젝트에서 수천 개의 단위 테스트를 수행하는 것은 드문 일이 아닙니다. 단위 테스트는 실행하는 데 시간이 거의 걸리지 않습니다. 밀리초.
• Isolated : 독립형 단위 테스트는 독립적으로 실행될 수 있으며, 파일 시스템 또는 데이터베이스와 같은 외부 요인에 종속되지 않습니다.
• Repeatable : 단위 테스트를 실행하는 것은 해당 결과와 일치해야 합니다. 즉, 실행 사이에 아무것도 변경하지 않으면 항상 동일한 결과를 반환합니다.
• Self-validating : 테스트는 사람의 개입 없이 통과했는지 여부를 자동으로 검색할 수 있어야 합니다.
• Timely : 위 테스트는 테스트 중인 코드에 비해 작성하는 데 불균형적으로 긴 시간이 걸리지 않아야 합니다.

마무리

오늘은 유닛 테스트에 대해 알아봤습니다. 개인적으로 유닛 테스트는 정말 주요하다고 생각합니다. 예전에 프로그램을 만들어 외국의 업체에 배포한 경험이 있습니다. 그때 유닛 테스트는 하지 않고 배포했었습니다. 그 당시 1년 차 개발자였고.. 그 당시 회사에서는 코드에 유닛 테스트를 도입하지 않았었습니다. 그때 나름 검증하고, 회사의 다른 PC에서도 검증을 했는데... 그 외국 업체의 PC에서 프로그램이 동작하지 않는다고 했습니다. 알고 보니 전역 변수로 선언한 변수를 초기화 하지 않고 사용 했었는데.. 보통 전역 변수는 선언과 동시에 0으로 초기화 됩니다. 근데 제가 실수로 그 변수를 초기화 하지 않고 0으로 가져다 썼습니다. 그 당시 프로그램에 문제는 없었습니다. 하지만... 모든 PC가 전역 변수를 0으로 초기화 하지 않더라고요... C++ 표준에는 전역변수를 0으로 초기화 하지만 일부 PC의 컴파일러에 따라 전역변수가 0으 초기화 되는걸 보장하지 않는다고 합니다.. 제가 분명 실수를 하고, 우연히 전역변수로 선언한 변수가 제가 사용하려는 0 값과 같이 겹치며 생긴 버그였습니다. 이때 욕 정말 많이 먹었습니다. 그 당시 저는 나름 검증을 했고 디버깅 시 이상이 없었기 때문에 외국업체에 너네 문제인 것 같다고 피드백을 줬는데.. 정말 개망신당했습니다. 하지만 이때 유닛 테스트를 했다면 충분히 걸러질 수 있는 버그였습니다. 그렇기 때문에 유닛 테스트는 배포 전 최소한의 검증 도구라고 생각합니다.
그럼 이상으로 포스팅 마치겠습니다. 감사합니다.

Intro

안녕하세요, 오늘은 python의 type hint에 대해서 알아보겠습니다.

python의 장점은 우리가 정의한 변수들의 타입을 알아서 동적으로 정해주는 것이죠. 하지만 이는 양날의 검이라고 볼 수있습니다. 프로그램 복잡도가 높아질수록, 많은 사람과 협업할수록 변수의 type을 파악해야 사전에 디버그할 수 있고, 적절한 로직을 짤 수 있습니다.

따라서 python에서는 이런 단점을 보완하기 위해서 type hint (a.k.a annotation) 라는 기능을 지원합니다. 이 변수의 type은 무엇인지, 또는 이 함수의 인수는 어떤 type이고, 어떤 type의 결과를 return하는지 명시해주는 것입니다. 이는 강제성은 없지만, mypy와 같은 type checker 또는 pycharm같은 IDE에서 검사를 해서 명시해준 type의 변수, 인수, 리턴 값이 나오지 않으면 경고를 보내줍니다.

하지만 이또한 강건한 프로그래밍이 가능하게 장점과 함께, 개발자의 노력과 시간이 더 소비된다는 단점도 있습니다. 저는 장점이 더 크다고 생각하기 때문에 Real Python 에 정리된 type hint 사용법을 보고 이글에 정리하고자 합니다.

Example1

원기둥 (cylinder)의 부피를 구하는 함수를 구현해보겠습니다. 원기둥의 부피를 구하는 공식은 $\pi r^2h$이고, 반지를 $r$과 높이 $h$만 알면 구할 수 있습니다. type hint를 적용해서 구현해보면 아래와 같습니다.

PI: float = np.pi

def get_cylinder_volume(radius: float, height: float = 1.) -> float:
    return PI * np.power(radius, 2) * height

get_cylinder_volume(2)
>> 12.566370614359172

get_cylinder_volume(int(2), 2)
>> 25.132741228718345

get_cylinder_volume.__annotations__
>> {'radius': float, 'height': float, 'return': float}

여기서 볼 point는 4가지 입니다.

1. 처음 변수 PI를 선언할 때 type hint를 적용했습니다. :을 통해 type을 명시할 수 있습니다.
2. get_cylinder_volume의 인수 type을 정해주고, return 값의 type은 float이라고 hint를 줬습니다.
3. type hint와 다른 type의 인수가 전해진다고 해서 에러가 발생하지 않습니다. 하지만 type hint를 지키짐 않으면 나중에 어딘가에서는 에러가 발생할 수도 있겠죠!
4. 함수의 __annotations__를 호출하면, 주어진 hint에 대한 정보가 저장되어있음을 할 수 있습니다. type checker 프로그램들은 이를 참고하겠죠?

추가) 함수가 어떤 값을 반환하지 않는 경우, -> None을 써줄수도 있고, 아예 안적어주는 것도 괜찮습니다.

Example2

float, int, str같은 기본적인 type 쉽게 hint를 줄 수 있지만, list, tupel, dict와 같은 경우는 추가적인 정보가 필요합니다. 단지 list로 끝날게 아니라, 어떤 type의 값들로 구성되어 있는지도 알아야 합니다. 따라서 이런 추가적인 정보를 제공하기 위해서는 typing모듈의 도움을 받아야 합니다. 위 제가 참고한 사이트의 예시를 인용하겠습니다.

from typing import Dict, List, Tuple

names: List[str] = ["Guido", "Jukka", "Ivan"]
version: Tuple[int, int, int] = (3, 7, 1)
options: Dict[str, bool] = {"centered": False, "capitalize": True}

3가지 변수와 type hint로 아래와 같이 정보를 알 수 있습니다.

1. name: str type의 변수로 이루어진 list
2. version: 3개의 값을 갖고있고, 3개 모두 int type 변수인 tuple, 값의 개수와 hint의 개수가 맞지 않으면 경고가 나갑니다.
3. options: key값은 str, value값은 bool인 dict

추가) 다루고자 하는 data가 list, tuple 둘 다 상관 없을 때는 좀 더 상위 개념인 Sequence를 사용할 수 있습니다. 하지만 웬만하면 정확하고, 통일성있도록 하는게 좋습니다.
추가) 만약 여러 type의 값을 갖고있는 list의 경우, List[Any], 또는 List[Union[int, str]]등으로 표현할 수 있습니다. 좀 더 명확한 Union이 더 좋을 거 같네요.

Example3

typing 모듈에서는 TypeVar라는 특별한 Type variable이 있습니다. 이는 상황에 따라서 어떤 type의 변수를 받을 수 있는 변수입니다. TypeVar은 주어진 값들을 모두 아우르면서 가장 specific한 type을 취합니다. 참고한 사이트의 예시를 인용하겠습니다.

아래와 같이 주어진 Sequence의 값 중 임의로 하나를 선택해주는 choose라는 함수를 정의했습니다.

import random
from typing import Sequence, TypeVar

Choosable = TypeVar("Choosable")

def choose(items: Sequence[Choosable]) -> Choosable:
    return random.choice(items)

주어지는 input에 따라 결정되는 Choosable의 type은 아래와 같습니다.

# str only
choose(["Guido", "Jukka", "Ivan"]) 
> Choosable: str
# int only
choose([1, 2, 3]) 
> Choosable: int
# bool & int & float
choose([True, 42, 3.14]) 
> Choosable: float
# str & int
choose(["Python", 3, 7]) 
> Choosable: object

마지막 예시에서는 str과 int사이의 공통 parent class가 없기 때문에 최상위 클래스인 object로 결정되었습니다.

만약 Choosable = TypeVar("Choosable", str, float) 처럼 선언하면, 마지막 예시처럼 정해지는 type이 str 또는 float이 아닌 경우에는 (int는 float의 하위 클래스라서 괜찮습니다.) 경고가 발생합니다.

마무리

오늘은 python의 type hint에 대해서 알아봤습니다. 오늘 소개한 것 말고도 함수를 인수로 넘겨줬을 때 줄 수 있는 hint인 Callable, 그리고 기본적으로 None을 내장하고 있어서 처음에는 None으로 초기화하고 나중에 값을 할당하고 싶을 때 사용할 수 있는 Optional hint도 있습니다.

글 읽어주셔서 감사합니다!

References

Python3.9 typing docs
[Real Python] type checking

Intro

안녕하세요, 오늘은 python의 built-in 모듈 중 하나인 timeit에 대해서 소개해드리겠습니다.

timeit은 우리가 작성한 코드의 실행 시간을 측정하는데 사용됩니다. 우리가 작성하고자 하는 로직을 구현하는 방법이 여러 가지가 있을 때, 더 빠른 방법을 선택하기 위한 테스트를 진행할 때 timeit을 사용합니다.

timeit을 사용하는 방법은 크게 두가지가 있습니다.

1. timeit모듈 import해서, timeit.timeit() 사용하기
2. IPython magic command %%timeit 사용하기

저는 jupyter notebook에서 두 번째 방법을 이용해서 수행 시간을 비교하는 테스트를 해보겠습니다.

Test1: list comprehension vs. map function

python의 기본 기능인 list comprehesion과 map의 속도를 비교해보겠습니다.

%%timeit
"-".join([str(n) for n in range(100000)])
>> 21.7 ms ± 1.37 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

%%timeit
"-".join(map(str, range(100000)))
>> 17.1 ms ± 653 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

map이 list comprehension보다 빠른 것을 확인할 수 있습니다. 여기서 한가지 차이 점은, list comprehension 실험 결과는 10 loops, map 실험 결과는 100 loops를 돌았다고 나옵니다. 이는 %%timeit magic command를 사용해서 속도를 측정할 때, 정확한 측정을 위해 해당 코드를 여러 번 실행해서 걸리는 시간을 평균냅니다. 그리고 이 숫자는 연산의 복잡도에 따라서 자동으로 정해집니다. (간단한 연산은 더 많이, 복잡한 연산은 더 조금)

위 실험의 경우 map 실험이 복잡도가 더 낮은 연산으로 구분되어서, list comprehension실험보다 많은 loop가 돈 것을 확인할 수 있습니다.

만약에 loop수를 통일하고 싶다면, -n [NUM_LOOPS] 인자를 주면 됩니다. 아래처럼요

%%timeit -n 10
"-".join(map(str, range(100000)))
>> 17.7 ms ± 1.33 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

Test2: (pandas) list comprehension vs. map function

pandas DataFrame에도, 특정 columns의 값에 동일한 함수를 적용시켜주는 map함수가 존재합니다. 하지만 듣기로는 pandas의 map함수는 잘 설계되어있지 않다고 들었는데요, 실제로 그런지 확인해보겠습니다.

아래와 같이 데이터를 준비하겠습니다.

import pandas as pd
import numpy as np

data_2d = np.random.rand(100000, 5)
df = pd.DataFrame(data_2d, columns=[f'data{idx}' for idx in range(len(data_2d[1]))])
df.head()

>>  data0        data1        data2        data3        data4
0    0.275805    0.693519    0.644440    0.277043    0.173847
1    0.598473    0.796305    0.106011    0.824349    0.061107
2    0.664825    0.998174    0.575312    0.225689    0.274685
3    0.577050    0.705411    0.800339    0.623300    0.254203
4    0.828888    0.291775    0.347555    0.277151    0.27

그리고 값을 소수점 2자리 까지만 고려해주는 round_value함수를 정의해준 뒤, list comprehension과 map의 속도를 비교해보겠습니다.

def round_value(x):
    return np.round(x, 2)

%%timeit
df['data0'].map(round_value)
>> 989 ms ± 17.2 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)


%%timeit
[round_value(value) for value in df['data0'].values]
>> 692 ms ± 38.6 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

소문이 사실이었습니다. pandas의 경우, map보다 list comprehension의 속도가 훨씬 빨랐습니다!

map을 사용했을 때 코드 가독성이 더 좋긴 하지만, 속도가 큰 차이가 나니 앞으로는 list comprehension을 사용하는 것이 좋겠네요.

Test3: (pandas) loc( ) vs. at( ) vs. iloc( ) vs. iat( )

위 4가지 함수들은 모두 DataFrame상에서 특정위치의 값을 가져오거나, 바꿀 때 사용할 수 있습니다.

앞에 i가 붙은 함수들을 index를 통해서만 접근이 가능하고, 그렇지 않는 함수들은 column 이름 등을 통해서 접근이 가능합니다.

또한 (i)at과 (i)loc의 차이점은, 한 번에 하나의 값에 접근할 것인지, 여러 값에 접근할 것인지에 따라 차이가 있습니다. 즉, (i)at가 하나의 값을 찾거나 수정하는데 더 특화되어 있다고 볼 수 있습니다.

바로 속도 비교 실험을 진행하겠습니다.

# at
%%timeit
[df.at[idx, 'data1'] for idx in df.index]
>> 401 ms ± 31.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

# loc
%%timeit
[df.loc[idx, 'data1'] for idx in df.index]
>> 661 ms ± 13 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

# iat
%%timeit
[df.iat[idx, 1] for idx in df.index]
>> 1.9 s ± 22.6 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

# iloc
%%timeit
[df.iloc[idx, 1] for idx in df.index]
>> 2.16 s ± 16.7 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)

실험 결과, (i)loc보다는 (i)at이 빠르고, i로 시작하는 함수보다는 그렇지 않은 함수가 더 빠르단 걸 알 수 있습니다. 신기하네요, 상황에 따라서 i가 붙은 함수를 사용할 수 있겠지만, 가능하면 하나의 값만 가져올 때는 at, 여러 개의 값을 가져올 때는 loc를 사용하는 것이 좋겠네요.

마무리

오늘은 python의 timeit 모듈에 대해서 알아보고, 평소에 궁금했던 것들을 테스트해 봤습니다. 글 읽어주셔서 감사합니다!

References

Python3.8 timeit docs
IPython timeit magic commands

Intro

안녕하세요. 이번 포스팅에서는 Visual studio2019 C++ 프로젝트에서 Unit test framework 중 하나인 Google test 연동 방법에 대해 포스팅하겠습니다. Google Test는 C++ Unit test에서 많이 쓰이는 framework입니다. 잘만 활용한다면 개발자의 실수를 최소화 할 수 있고 경건한 프로그램을 만들 수 있습니다.

Visual studio2019 google test 연동방법

1) 테스트 프로젝트 생성테스트 할 프로젝트를 생성하고 코드를 작성해줍니다. 간단한 테스만 수행하기 위해 math class에 메서드로 sum과 multiply을 구현 하였습니다.

math.h
class math
{
public:
    int math::sum(int a, int b);
    int math::multiply(int a, int b);

}

간단하게 sum함수와 multiply함수를 테스트해보겠습니다.

 math.c

 #include "math.h"
int math::sum(int a, int b)
{
    return a + b;
}
int math::multiply(int a, int b)
{
    return a * b;

}
     (adsbygoogle = window.adsbygoogle || []).push({});

2) lib파일 생성 (구성 형식. exe -> lib 변경)exe파일이 아닌 lib파일로 변경하는 이유는 테스트 할 프로젝트 솔루션의 header만 가져다 쓰기 위해서입니다.

3) Google test 프로젝트 생성

3-1) 새 프로잭트 생성

3-2) Google Test 선택

3-3) 프로젝트 생성

3-4) 프로젝트 생성옵션 선택 (정적 라이브버리(.lib), 동적으로 연결 선택)

3-5) 처음 Google Test 프로젝트 만들었을 때 화면

3-6) 시작 프로잭트 변경. 프로젝트 -> 속성 -> 시작 프로젝트 -> Sample-Test1 변경

3-7) 기본 빌드 결과

4) Test 프로젝트 연동

4-1) 링커 경로 포함 (google test project -> 속성 -> 링커 -> 일반 -> 추가 라이브러리 디렉터리 -> ..\x64\Debug 추가)

4-2) lib파일 추가. 테스트할 프로젝트의 lib파일 추가하기 위한 lib path입니다.링커 -> 입력 -> 추가 종속성 -> 라이브러리 추가 (gtest.lib, gtest_maind.lib, Unit_Test.lib)

gtest.lib와 gtest_maind.lib는 google test에 포함되어 있는 lib입니다. lib path는 개인 마음대로입니다. 저는 따로 만들기 귀찮아서 저 폴더에 넣었습니다.

5) Test case 작성

5-1) test case 작성테스트할 프로젝트의 header을 include 하고 test case를 작성합니다. 결과를 보면 1번 case와 3번 case는 통과하게 하였고, 2번 case와 4번 case는 실패하게 케이스를 작성했습니다. 정상적으로 unit test가 수행됨을 확일 할 수 있습니다.

5-2) 빌드 결과

5-3) 테스크 탐색기 결과 (테스트 -> 테스트 탐색기)

6) 결과물 xml 파일로 만들기

자 이제 마지막입니다. test 한 산출물을 xml 파일로 만들어야 합니다.

6-1) visual studio에서 xml 파일 만들기

속성-> 구성 속성 -> 명령 인수 (--gtest_output=xml:..\x64\Debug\result.xml 입력)

결과

6-2) cmd에서 xml 파일 만들기

xml 파일 만들기는 명령 프롬프트로도 확인이 가능합니다

test실행 파일이 있는 폴더로 이동

Sample-Test 1.exe --gtest_output=xml:result2.xml 커맨드 입력

결과가 똑같이 만들어짐을 확일 할 수 있습니다. 보통 기업에서는 xml파일을 가공해서 산출물을 관리하기도 합니다. git에서 찾아보면 xml을 html코드로 바꾸는 방법이 많이 나와있습니다. 그쪽 참조해보시면 될 것 같습니다.

마무리

이번 포스팅에서는 visual studio 2019에서 Google Unit Test 하는 방법에 대해 알아 보았습니다. Unit test는 실제 개발자의 실수를 줄여줄 수 있는 방법입니다. 그리고 개인적으로 배포 전 꼭 거쳐야 하는 과정이라고 생각합니다.

그럼 이만 포스팅을 마치겠습니다.

감사합니다.